Question

【题目】已知抛物线y=ax2+bx+c的图象如图所示，根据图象解答下列问题：

（1）抛物线与x轴的另一个交点坐标；　 　；

（2）方程ax2+bx+c=0的两个根是　 　；

（3）不等式ax2+bx+c＜0的解是　 　；

（4）y随x的增大而减小的自变量x的取值范围是　 　；

（5）求出抛物线的解析式及顶点坐标．

Answer 1

【答案】（1）（3，0）；（2）x=﹣1或x=3；（3）﹣1＜x＜3；（4）x=1；（5）（1，﹣4）；

【解析】

（1）观察图象可知抛物线的对称轴为x=1，与x轴的一个交点坐标为（﹣1，0），根据抛物线的对称性即可求得抛物线与x轴的另一个交点坐标；（2）根据抛物线与x轴的两个交点坐标为（3，0）（﹣1，0），即可求得方程ax2+bx+c=0的两个根是x=﹣1或x=3；（3）已知抛物线与x轴的两个交点坐标为（3，0）（﹣1，0），观察图象即可得不等式ax2+bx+c＜0的解是﹣1＜x＜3；（4）观察图象即可解答；（5）利用待定系数法求得抛物线的解析式，再把解析式化为顶点式，即可求得顶点坐标．

（1）依题意得抛物线的对称轴为x=1，与x轴的一个交点坐标为（﹣1，0），

∴抛物线 与x轴的另一个交点坐标为（3，0）；

（2）∵抛物线与x轴的两个交点坐标为（3，0）（﹣1，0），

∴方程ax2+bx+c=0的两个根是x=﹣1或x=3；

（3）∵抛物线与x轴的两个交点坐标为（3，0）（﹣1，0），

∴不等式ax2+bx+c＜0的解是﹣1＜x＜3；

（4）∵抛物线的对称轴为x=1，

∴y随x的增大而减小的自变量x的取值范围是x＜1；

（5）依题意得抛物线与坐标轴的三个交点坐标为（3，0），（﹣1，0），（0，﹣3），

设抛物线的解析式为y=ax2+bx+c，

把三个点的坐标代入其中得，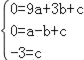

解之得，

∴y=x2﹣2x﹣3=（x﹣1）2﹣4，

∴顶点坐标为（1，﹣4）．