
【题目】如图,正方形MNPQ网格中,每个小方格的边长都相等,正方形ABCD的顶点在正方形MNPQ的小方格顶点上.

(1)设正方形MNPQ网格内的每个小方格的边长为1,求:
①△ABQ,△BCM,△CDN,△ADP的面积;
②正方形ABCD的面积;
(2)设MB=a,BQ=b,利用这个图形中的直角三角形和正方形的面积关系,你能验证勾股定理吗?相信你能给出简明的推理过程.
【答案】(1)①6;②25;(2)见解析
【解析】试题分析:(1)根据直角三角形的面积公式:S=两条直角边的乘积的一半进行计算;
(2)根据面积能够验证勾股定理.
试题解析:解:(1)∵网格中每个小正方形的边长为1,由图可知AQ=3,BQ=4,∠Q=90°,∴S△ABQ=![]() AQBQ=6;同理S△BCM=S△CDN=S△ADP=6.
AQBQ=6;同理S△BCM=S△CDN=S△ADP=6.
又∵MQ=7,∴S正方形MNPQ=49,∴S正方形ABCD=S正方形MNPQ﹣4S△ABQ=49﹣4×6=25.
(2)能够验证勾股定理.理由如下:
在△BCM、△ABQ中,∵∠M=∠Q=∠ABC=90°,∴∠MBC=∠QAB.
又∵AB=BC,∴△BCM≌△ABQ.
同理△CDN≌△DAP≌△BCM.
∵MB=a,BQ=b,S正方形ABCD=S正方形MNPQ﹣4S△ABQ,∴AB2=(a+b)2﹣4×![]() ab,即AB2=a2+b2.
ab,即AB2=a2+b2.
设AB=c,得c2=a2+b2.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标中表示下面各点:A(0,3),B(1,﹣3),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,7).
①A点到原点O的距离是________ .
②将点C向x轴的负方向平移6个单位它与点________重合.
③连接CE,则直线CE与y轴位置关系是________ .
④点F分别到x、y轴的距离分别是________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:
甲 | 85 | 88 | 84 | 85 | 83 |
乙 | 83 | 87 | 84 | 86 | 85 |
(1)请你分别计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万美服装店准备购进一批两种不同型号的衣服,已知若购进A型号的衣服9件,B型号的衣服10件共需1 810元;若购进A型号的衣服12件,B型号的衣服8件共需1 880元.已知销售一件A型号的衣服可获利18元,销售一件B型号的衣服可获利30元.
(1)求A、B型号衣服的进价各是多少元?
(2)若已知购进的A型号的衣服比B型号衣服的2倍还多4件,且购进的A型号的衣服不多于28件,则该服装店要想获得的利润不少于699元,在这次进货时可有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是 . 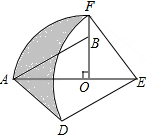
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )

A. 110° B. 120° C. 130° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为<x>,即当n为非负整数时,若![]() ,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
,则<x>=n,如<0.46>=0,<3.67>=4。给出下列关于<x>的结论:
①<1.493>=1;
②<2x>=2<x>;
③若![]() ,则实数x的取值范围是
,则实数x的取值范围是![]() ;
;
④当x≥0,m为非负整数时,有![]() ;
;
⑤![]() 。
。
其中,正确的结论有 (填写所有正确的序号)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com