
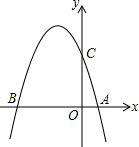
 如图,抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.
如图,抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.
|
|
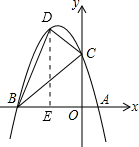 (2)在该抛物线位于第二象限的部分上是否存在点D,使得△DBC的面积S最大.理由如下:
(2)在该抛物线位于第二象限的部分上是否存在点D,使得△DBC的面积S最大.理由如下:| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
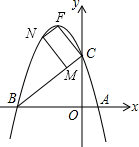 (3)能够在直线BC上找到一个点M,在抛物线上找到一个点N,使得C、F、M、N四点组成的四边形为平行四边形.理由如下:
(3)能够在直线BC上找到一个点M,在抛物线上找到一个点N,使得C、F、M、N四点组成的四边形为平行四边形.理由如下:| 3 |
| 2 |
| 25 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
| 31 |
| 4 |
| 31 |
| 4 |
|
|
|
| 5 |
| 2 |
| 21 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
| 21 |
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
| 21 |
| 4 |
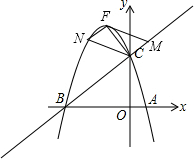 x=1不合题意舍去,
x=1不合题意舍去,| 5 |
| 2 |
| 21 |
| 4 |
| 5 |
| 2 |
| 21 |
| 4 |


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
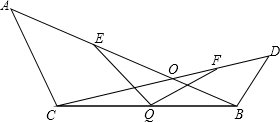 如图,已知:AB、CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE、QF,试探讨QE、QF的大小关系,并说明理由.
如图,已知:AB、CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE、QF,试探讨QE、QF的大小关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
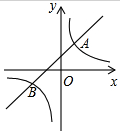 如图,直线y=x+2与双曲线y=
如图,直线y=x+2与双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 右图为手的示意图,在各个手指间标记字母 A,B,C,D.请你按图中箭头所指方向(即 A→B→C→D→C→B→A→B→C→…的方式)从 A 开始数连续的正整数 1,2,3,4,…,当字母C第2n+1次出现时(n为正整数),恰好数到的数是
右图为手的示意图,在各个手指间标记字母 A,B,C,D.请你按图中箭头所指方向(即 A→B→C→D→C→B→A→B→C→…的方式)从 A 开始数连续的正整数 1,2,3,4,…,当字母C第2n+1次出现时(n为正整数),恰好数到的数是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com