
【题目】如图,在长方形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )

A.4B.5C.![]() D.
D.![]()
【答案】C
【解析】
设CE=x,由矩形的性质得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折叠的性质得出BF=BC=5,EF=CE=x,DE=CD-CE=3-x.在Rt△ABF中利用勾股定理求出AF的长度,进而求出DF的长度;然后在Rt△DEF根据勾股定理列出关于x的方程即可解决问题.
解:设CE=x.
∵四边形ABCD是矩形,
∴AD=BC=5,CD=AB=3,∠A=∠D=90°.
∵将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,
∴BF=BC=5,EF=CE=x,DE=CD-CE=3-x.
在Rt△ABF中,由勾股定理得:
AF2=52-32=16,
∴AF=4,DF=5-4=1.
在Rt△DEF中,由勾股定理得:
EF2=DE2+DF2,
即x2=(3-x)2+12,
解得:x=![]() ,
,
故选C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是______形,根据的数学原理是:_______________________;
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是_______形,根据的数学原理是:_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=![]() 的图象与双曲线y=
的图象与双曲线y=![]() (k≠0,x>0)相交于点A(3,m)和点B.
(k≠0,x>0)相交于点A(3,m)和点B.
(1)求双曲线的解析式及点B的坐标;
(2)若点P在y轴上,连接PA,PB,求当PA+PB的值最小时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,平行四边形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 的延长线于点
的延长线于点![]() ,连结
,连结![]() .
.

![]() 求证:
求证:![]() ;
;
![]() 当平行四边形
当平行四边形![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是菱形?证明你的结论.
是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在用描点法画二次函数![]() 的图象时,列出下面的表格:
的图象时,列出下面的表格:
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
根据表格提供的信息,下列说法错误的是( )
A. 该抛物线的对称轴是直线![]() B. 该抛物线与
B. 该抛物线与![]() 轴的交点坐标为
轴的交点坐标为
C. ![]() D. 若点
D. 若点![]() 是该抛物线上一点.则
是该抛物线上一点.则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴仅有一个公共点
轴仅有一个公共点![]() ,经过点
,经过点![]() 的直线交该抛物线于点
的直线交该抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且点
,且点![]() 是线段
是线段![]() 的中点.
的中点.

![]() 求这条抛物线对应的函数解析式;
求这条抛物线对应的函数解析式;
![]() 求直线
求直线![]() 对应的函数解析式.
对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
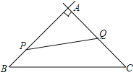
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,现有动点
,现有动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,动点
方向运动,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向运动,已知点
方向运动,已知点![]() 的速度是
的速度是![]() ,点
,点![]() 的速度是
的速度是![]() ,它们同时出发,经过________秒,
,它们同时出发,经过________秒,![]() 的面积是
的面积是![]() 面积的一半?
面积的一半?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中装有两个红色球,两个白色和一个蓝色球,这些球除颜色外都相同,从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球.
![]() 利用画树状图或列表的方法求摸到的两个球的颜色能配成紫色的概率(红色和蓝色可以配成紫色);
利用画树状图或列表的方法求摸到的两个球的颜色能配成紫色的概率(红色和蓝色可以配成紫色);
![]() 若将题干中的“记下颜色后放回”改为“记下颜色后不放回”,请直接写出摸到的两个球的颜色能配成紫色的概率.
若将题干中的“记下颜色后放回”改为“记下颜色后不放回”,请直接写出摸到的两个球的颜色能配成紫色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各个等式的规律:
第一个等式:22-12-1=2,第二个等式:32-22-1=4,第三个等式:42-32-1=6…请用上述等式反映出的规律解决下列问题:
(1)直接写出第四个等式;
(2)猜想第n个等式(用含n的式子表示),并证明你猜想的等式是正确的;
(3)直接写出20202-20192-2019=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com