
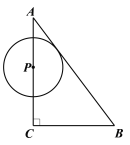
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 运动,速度为
运动,速度为![]() 个单位/
个单位/![]() ,在点
,在点![]() 运动的过程中,以
运动的过程中,以![]() 为圆心的圆始终与斜边
为圆心的圆始终与斜边![]() 相切,设⊙
相切,设⊙![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (
(![]() )(
)(![]() ).
).
(1)当![]() 时,
时,![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,直接写出t的值.
【答案】(1)7-t(2)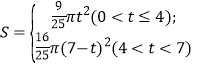 (3)
(3)![]()
【解析】
(1)先判断出点P在BC上,即可得出结论;
(2)分点P在边AC和BC上两种情况:利用相似三角形的性质得出比例式建立方程求解即可得出结论;
(3)分点P在边AC和BC上两种情况:借助(2)求出的圆P的半径等于PC,建立方程求解即可得出结论.
(1)∵AC=4,BC=3,∴AC+BC=7.
∵4<t<7,∴点P在边BC上,∴BP=7﹣t.
故答案为:7﹣t;
(2)在Rt△ABC中,AC=4,BC=3,根据勾股定理得:AB=5,由运动知,AP=t,分两种情况讨论:
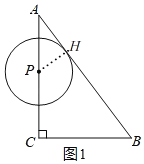
①当点P在边AC上时,即:0<t≤4,如图1,记⊙P与边AB的切点为H,连接PH,∴∠AHP=90°=∠ACB.
∵∠A=∠A,∴△APH∽△ACB,∴![]() ,∴
,∴![]() ,∴PH
,∴PH![]() t,∴S
t,∴S![]() πt2;
πt2;
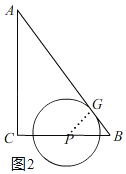
②当点P在边BC上时,即:4<t<7,如图,记⊙P与边AB的切点为G,连接PG,∴∠BGP=90°=∠C.
∵∠B=∠B,∴△BGP∽△BCA,∴![]() ,∴
,∴![]() ,∴PG
,∴PG![]() (7﹣t),∴S
(7﹣t),∴S![]() π(7﹣t)2.
π(7﹣t)2.
综上所述:S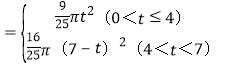 ;
;
(3)分两种情况讨论:
①当点P在边AC上时,即:0<t≤4,由(2)知,⊙P的半径PH![]() t.
t.
∵⊙P与△ABC的另一边相切,即:⊙P和边BC相切,∴PC=PH.
∵PC=4﹣t,∴4﹣t![]() t,∴t
t,∴t![]() 秒;
秒;
②当点P在边BC上时,即:4<t<7,由(2)知,⊙P的半径PG![]() (7﹣t).
(7﹣t).
∵⊙P与△ABC的另一边相切,即:⊙P和边AC相切,∴PC=PG.
∵PC=t﹣4,∴t﹣4![]() (7﹣t),∴t
(7﹣t),∴t![]() 秒.
秒.
综上所述:在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,t的值为![]() 秒或
秒或![]() 秒.
秒.


科目:初中数学 来源: 题型:
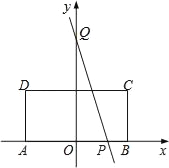
【题目】如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
A. ![]() 或-
或-![]() B.
B. ![]() 或-
或-![]() C.
C. ![]() 或-
或-![]() D.
D. ![]() 或-
或-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
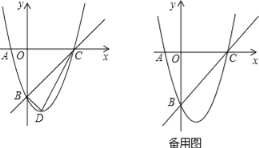
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
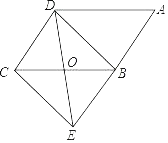
【题目】如图,在ABCD,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD、EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠BOD=100°,则当∠A= 时,四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山种植某产品种蜜柚![]() 已知该蜜柚的成本价为8元
已知该蜜柚的成本价为8元![]() 千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量
千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量![]() 千克
千克![]() 与销售单价
与销售单价![]() 元
元![]() 千克
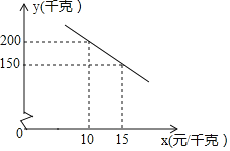
千克![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
![]() 求y与x的函数关系式,并写出x的取值范围;
求y与x的函数关系式,并写出x的取值范围;
![]() 当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线y=2x+2与x轴,y轴分别交于A,B两点,与反比例函数y=![]() (x>0)的图象交于点M(a,4).
(x>0)的图象交于点M(a,4).
(1)求反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)若点C在反比例函数y=![]() (x>0)的图象上,点D在x轴上,当四边形ABCD是平行四边形时,求点D的坐标.
(x>0)的图象上,点D在x轴上,当四边形ABCD是平行四边形时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△ACD,连接AD,BC.若∠ACB=30°,AB=1,CC=x,则下列结论:①△AAD≌△CCB;②当x=1时,四边形ABCD是菱形;③当x=2时,△BDD为等边三角形.其中正确的是_______(填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com