
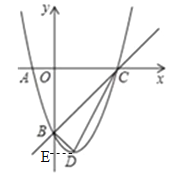
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状.
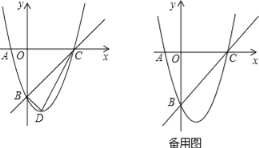
【答案】(1)y=x2-2x-3;(2)C(3,0),D(1,-4),△BCD是直角三角形.
【解析】
(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x轴的交点,再判断出△BOC和△BED都是等腰直角三角形,从而得到结论.
(1)∵x2+4x+3=0,∴x1=﹣1,x2=﹣3.
∵m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3.
∵抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),∴![]() ,∴
,∴![]() ,∴抛物线解析式为y=x2﹣2x﹣3;
,∴抛物线解析式为y=x2﹣2x﹣3;
(2)令y=0,则x2﹣2x﹣3=0,∴x1=﹣1,x2=3,∴C(3,0).
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴顶点坐标D(1,﹣4).
过点D作DE⊥y轴.
∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
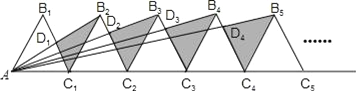
【题目】如图,(n+1)个边长为2的等边三角形△B1AC1,△B2C1C2、△B2C2C3,…,△Bn+1CnCn+1有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,△B4D3C3的面积为S3,…,△Bn+1DnCn的面积为Sn,则S2016=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
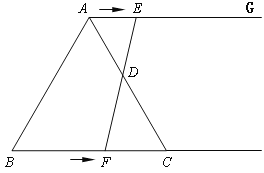
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空:当t为_________s时,四边形ACFE是菱形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y1=a(x﹣h)2+2,直线1:y2=kx﹣kh+2(k≠0).
(1)求证:直线l恒过抛物线C的顶点;
(2)若a>0,h=1,当t≤x≤t+3时,二次函数y1=a(x﹣h)2+2的最小值为2,求t的取值范围.
(3)点P为抛物线的顶点,Q为抛物线与直线l的另一个交点,当1≤k≤3时,若线段PQ(不含端点P,Q)上至少存在一个横坐标为整数的点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
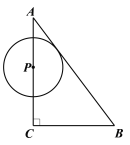
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 运动,速度为
运动,速度为![]() 个单位/
个单位/![]() ,在点
,在点![]() 运动的过程中,以
运动的过程中,以![]() 为圆心的圆始终与斜边
为圆心的圆始终与斜边![]() 相切,设⊙
相切,设⊙![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (
(![]() )(
)(![]() ).
).
(1)当![]() 时,
时,![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
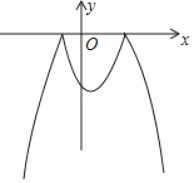
【题目】已知二次函数y=﹣x2+x+6及一次函数y=x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=x+m与这个新图象有四个交点时,m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
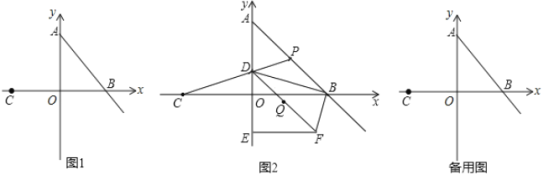
【题目】如图1,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)如图2,点![]() 在线段
在线段![]() (不包括
(不包括![]() ,
,![]() 两点)上,连接
两点)上,连接![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.![]() 、
、![]() 的垂直平分线交于点
的垂直平分线交于点![]() ,连接
,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,作
,作![]() 轴于
轴于![]() ,连结
,连结![]() .求证:
.求证:![]() ;
;
(3)在(2)的条件下,当![]() 的边
的边![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com