
【题目】如图,在等边三角形![]() 中,
中,![]() 是高,点
是高,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,下列说法中正确的有__________(填序号)
,下列说法中正确的有__________(填序号)
①![]() , ②
, ②![]() , ③
, ③![]() ,④
,④![]() .
.
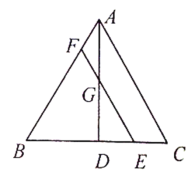
【答案】①②④
【解析】
先根据等边三角形的性质得出∠DAC=30°,再由平行线的性质可得出∠AGF的度数为30°,得出①正确;再由![]() 得出
得出![]() ,故②正确;根据△BEF∽△BCA得出EF和AC之比,再结合GE和AC之比得出GE和FG的关系为:
,故②正确;根据△BEF∽△BCA得出EF和AC之比,再结合GE和AC之比得出GE和FG的关系为:![]() ,故④正确;再根据AD和BD的关系,以及AG和DG的关系可以得出BD和DG的关系为DG=
,故④正确;再根据AD和BD的关系,以及AG和DG的关系可以得出BD和DG的关系为DG=![]() BD,故③错误.
BD,故③错误.
解:∵△ABC为等边三角形,
∴∠BAC=60°,
又∵AD是高,
∴∠DAC=30°,
∵![]() ,
,
∴∠DGE=∠DAC=∠AGF=30°,△DGE∽△DAC,故①正确,
∵点E为CD中点,
∴![]() ,
,
∴![]() ,故②正确,
,故②正确,
∵![]() ,
,
∴△BEF∽△BCA,
∵E为CD中点,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,故④正确,
,故④正确,
∵AD=![]() BD,DG=
BD,DG=![]() AD,
AD,
∴DG=![]() BD,故③错误.
BD,故③错误.
故答案为:①②④.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于![]() BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
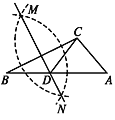
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
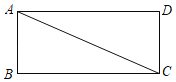
【题目】如图,有一个长方形花园,对角线AC是一条小路,现要在AD边上找一个位置建报亭H,使报亭H到小路两端点A、C的距离相等.
(1)用尺规作图的方法,在图中找出报亭H的位置(不写作法,但需保留作图痕迹,交代作图结果)
(2)如果AD=80m,CD=40m,求报亭H到小路端点A的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
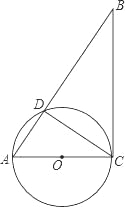
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 两村在一条小河的同一侧,要在河边建水厂向两村供水.
两村在一条小河的同一侧,要在河边建水厂向两村供水.
(1)若要使自来水厂到两村的距离相等,厂址![]() 应选在哪个位置?
应选在哪个位置?
(2)若要使自来水厂到两村的输水管用料最省,厂址![]() 应选在哪个位置?
应选在哪个位置?
(3)自来水厂建好后,在招收职工的试卷中有道题“请你在河流![]() 上找出一点
上找出一点![]() ,使
,使![]() 的值最大.”你能找到
的值最大.”你能找到![]() 点吗?请将上述
点吗?请将上述![]() 三点在下列各图分别标出,并保留尺规作图痕迹.
三点在下列各图分别标出,并保留尺规作图痕迹.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个筑路队共同承担一段一级路的施工任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用15天.且甲队单独施工60天和乙队单独施工40天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了4天后,乙队因设备检修停止施工,由甲队单独继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=10,BC=16,AD是BC边上的中线且AD=6,![]() 是AD上的动点,
是AD上的动点,![]() 是AC边上的动点,则
是AC边上的动点,则![]() 的最小值是( ).
的最小值是( ).

A.![]() B.16C.6D.10
B.16C.6D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:我们将能完全覆盖三角形的最小圆称为该三角形的最小覆盖圆.若三角形为锐角三角形,则其最小覆盖圆为其外接圆;若三角形为直角或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆.问题:能覆盖住边长为![]() 、
、![]() 、
、![]() 的三角形的最小圆的直径是________.
的三角形的最小圆的直径是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com