
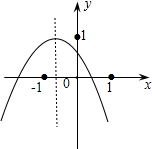
 小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据图象与x的交点的个数,判断根的判别式△>0;②取x=0时,y=c>0但c<1;③对称轴方程x=-$\frac{b}{2a}$,图象开口方向判断a与0的关系,再判断b与0的关系;④取x=-1时,y=a-b+c>0.
解答 解:①因为二次函数图象与x轴有两个交点,所以根的判别式b2-4ac>0.故①正确;
②根据图象知,当x=0时,0<y<1,即0<c<1;故②不正确;
③由该函数的图象知,开口向下,
∴a<0;
对称轴方程x=-$\frac{b}{2a}$<0,
∴b<0,
∴ab>0.故③正确;
④根据图象可知,当x=-1时,y>0,
所以a-b+c>0.
故④不正确;
综上所述,正确共2个.
故选B.
点评 本题考查了图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:选择题
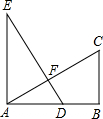 如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )
如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB的中点,以下判断正确的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 0 | 3 | 4 | 3 | 0 | -5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.
如图,从直径为2cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是$\frac{\sqrt{2}}{4}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
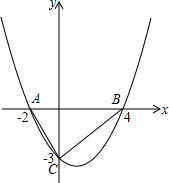 如图,二次函数的图象经过A、B、C三点
如图,二次函数的图象经过A、B、C三点查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
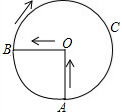 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )
某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )| A. | 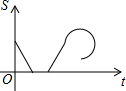 | B. | 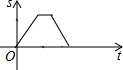 | C. | 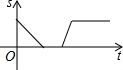 | D. | 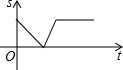 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
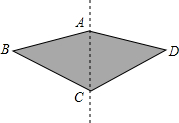 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com