
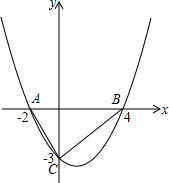
 如图,二次函数的图象经过A、B、C三点
如图,二次函数的图象经过A、B、C三点分析 (1)根据A与B坐标设出二次函数解析式为y=a(x-4)(x+2),把C坐标代入求出a的值,即可确定出解析式;
(2)存在,由三角形PAB与三角形ABC面积相等,底都为AB,得到C纵坐标绝对值与P纵坐标绝对值相等,确定出P坐标即可.
解答 解:(1)由A(-2,0),B(4,0),设二次函数解析式为y=a(x-4)(x+2),
把C(0,-3)代入得:-3=-8a,即a=$\frac{3}{8}$,
则抛物线解析式为y=$\frac{3}{8}$(x-4)(x+2)=$\frac{3}{8}$x2-$\frac{3}{4}$x-3;
(2)根据题意得:|P纵坐标|=3,即P纵坐标=3或-3,
把y=3代入抛物线解析式得:3=$\frac{3}{8}$x2-$\frac{3}{4}$x-3,
解得:x=6或x=-4,此时P坐标为(6,3)或(-4,3);
把y=-3代入抛物线解析式得:-3=$\frac{3}{8}$x2-$\frac{3}{4}$x-3,
解得:x=0(与C重合,舍去)或x=2,此时P坐标为(2,-3).
点评 此题考查了待定系数法求二次函数解析式,以及二次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | S=x(20-x) | B. | S=x(20-2x) | C. | S=10x-x2 | D. | S=2x(10-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
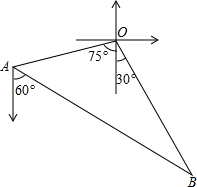 如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
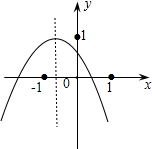 小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )
小李从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面四条信息:①b2-4ac>0;②c>1;③ab>0;④a-b+c<0.你认为其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
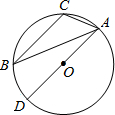 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为12,sinB=$\frac{1}{4}$,则线段AC的长度是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为12,sinB=$\frac{1}{4}$,则线段AC的长度是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
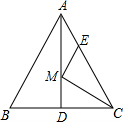 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )| A. | $\sqrt{26}$ | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{7}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com