
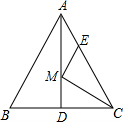
 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )| A. | $\sqrt{26}$ | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{7}$ | D. | 4$\sqrt{2}$ |
分析 在AB上取AE′=AE,连接CE′,过点E′作E′F⊥BC由等边三角形的性质可知:AB=AC=BC=6,∠B=60°,然后证明△AE′M≌△AEM,从而得到E′M=EM,由两点之间线段最短可知:当E′、M、C在一条直线上时,EM+MC有最小值,在Rt△E′BF中,可求得BF=2,E′F=2$\sqrt{3}$,最后在Rt△E′FC中,由勾股定理求E′C的长即可.
解答 解:如图所示,在AB上取AE′=AE,连接CE′,过点E′作E′F⊥BC.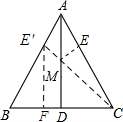
∵△ABC为等边三角形,
∴AB=AC=BC=6.
∵AB=AC,AD是BC边上的中线,
∴∠BAD=∠CAD.
在△AE′M和△AEM中,
$\left\{\begin{array}{l}{AE′=AE}\\{∠E′AM=∠EAM}\\{AM=AM}\end{array}\right.$,
∴△AE′M≌△AEM,
∴E′M=EM.
由两点之间线段最短可知:当E′、M、C在一条直线上时,EM+MC有最小值.
∵AE=2,
∴BE′=AB-AE′=4
在Rt△E′BF中,∠B=60°,
∴$\frac{BF}{BE′}=\frac{1}{2}$,$\frac{E′F}{BE′}$=$\frac{\sqrt{3}}{2}$.
∴BF=$\frac{1}{2}BE′=\frac{1}{2}×4=2$,E′F=$\frac{\sqrt{3}}{2}BE′$=$\frac{\sqrt{3}}{2}×4=2\sqrt{3}$.
∴FC=BC-BF=4.
在Rt△E′FC中,E′C=$\sqrt{E′{F}^{2}+F{C}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{4}^{2}}$=2$\sqrt{7}$.
∴EM+MC=2$\sqrt{7}$.
故选:C.
点评 本题主要考查的是等边三角形的性质、特殊锐角三角函数值的应用、轴对称-路径最短等知识点,明确当E′、M、C在一条直线上时,EM+MC有最小值是解题的关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数的图象经过A、B、C三点
如图,二次函数的图象经过A、B、C三点查看答案和解析>>
科目:初中数学 来源: 题型:选择题
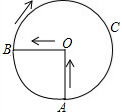 某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )
某景点有一座圆形的建筑,如图,小江从点A沿AO匀速直达建筑中心点O处,停留拍照后,从点O沿OB以同样的速度匀速走到点B,紧接着沿$\widehat{BCA}$回到点A,下面可以近似地刻画出小江与中心O的距离S随时间t变化的图象是( )| A. | 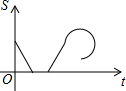 | B. | 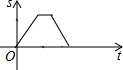 | C. | 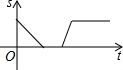 | D. | 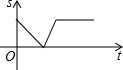 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
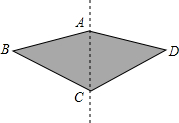 如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )
如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,那么∠D=∠B=40°,则∠BCD的度数是( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A(1,2),B(m,$\frac{1}{2}$)是双曲线上的点.
已知A(1,2),B(m,$\frac{1}{2}$)是双曲线上的点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com