
 ��֪A��1��2����B��m��$\frac{1}{2}$����˫�����ϵĵ㣮
��֪A��1��2����B��m��$\frac{1}{2}$����˫�����ϵĵ㣮���� ��1���跴��������ʽΪy=$\frac{k}{x}$����A������뷴��������ʽ���k��ֵ��ȷ��������������ʽ���ɣ�
��2����B������뷴��������ʽ���m��ֵȷ����B���꣬��ֱ��AB����ʽΪy=mx+n����A��B����������m��n��ֵ������ȷ����ֱ��AB����ʽ��
��3����������x���ϣ������������x������ֻ��һ�����㣬��������Ϊy=a��x-h��2����A��B����������a��h��ֵ������ȷ������������������߽���ʽ��
��4����i�������䷽�Ľ�������÷Ǹ����������������ʽ�ӵ���Сֵ���ɣ�
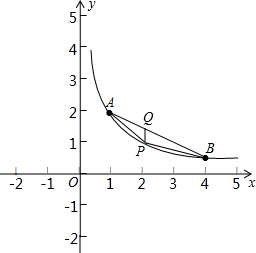
��ii����ͼ����P��m��$\frac{2}{m}$��Ϊ˫������AB�ε�����һ�㣬����P��PQ��y�ύAB�ڵ�Q����ʾ��Q���꣬������ʾ��PQ�ij�����ʾ��S��m�Ķ��κ�������ʽ�����ö��κ����������S�����ֵ���ɣ�
���  �⣺��1���跴��������ʽΪy=$\frac{k}{x}$��
�⣺��1���跴��������ʽΪy=$\frac{k}{x}$��
�ѵ�A��1��2������˫����y=$\frac{k}{x}$���ã�2=$\frac{k}{1}$����k=2��
�����A��B��˫����Ϊy=$\frac{2}{x}$��
��2���ߵ�B��m��$\frac{1}{2}$����˫����Ϊy=$\frac{2}{x}$�ϣ�
��m=4����B��4��$\frac{1}{2}$����
��ֱ��AB����ʽΪy=mx+n��
��A��B�������ã�$\left\{\begin{array}{l}{m+n=2}\\{4m+n=\frac{1}{2}}\end{array}\right.$��
��ã�m=-$\frac{1}{2}$��n=$\frac{5}{2}$��
�����A��B��ֱ�߷���y=-$\frac{1}{2}$x+$\frac{5}{2}$��
��3����������Ϊy=a��x-h��2��
�ѵ�A��B�����$\left\{\begin{array}{l}{a��h-1��^{2}=2}\\{a��h-4��^{2}=\frac{1}{2}}\end{array}\right.$��
��ã�a=$\frac{1}{18}$��h=7��a=$\frac{1}{2}$��h=3��
�����A��B��������x������ֻ��һ������������߽���ʽΪy=$\frac{1}{18}$��x-7��2��y=$\frac{1}{2}$��x-3��2��
��4����i����n��0��
��n+$\frac{4}{n}$=��$\sqrt{n}$-$\frac{2}{\sqrt{n}}$��2+4��4��
�����ʽn+$\frac{4}{n}$����Сֵ��4��
�ʴ�Ϊ��4��
��ii����ͼ����P��m��$\frac{2}{m}$��Ϊ˫������AB�ε�����һ�㣬
����P��PQ��y�ύAB�ڵ�Q����Q��m��-$\frac{1}{2}$m+$\frac{5}{2}$����
��PQ=-$\frac{1}{2}$m+$\frac{5}{2}$-$\frac{2}{m}$��
��S=$\frac{15}{4}$-$\frac{3}{m}$-$\frac{3m}{4}$=$\frac{15}{4}$-3��$\frac{1}{m}$+$\frac{m}{4}$����$\frac{15}{4}$-3=$\frac{3}{4}$��
���PAB����������ֵ��$\frac{3}{4}$��
���� �������ڷ����������ۺ��⣬�漰��֪ʶ�У�����ϵ������������ʽ��һ�κ�������ʽ���Ǹ��������ʣ��Լ���������ʽ�����ã��������մ���ϵ�����ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | S=x��20-x�� | B�� | S=x��20-2x�� | C�� | S=10x-x2 | D�� | S=2x��10-x�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
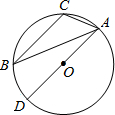 ��ͼ����O�ǡ�ABC�����Բ��AD�ǡ�O��ֱ��������O�İ뾶Ϊ12��sinB=$\frac{1}{4}$�����߶�AC�ij����ǣ�������
��ͼ����O�ǡ�ABC�����Բ��AD�ǡ�O��ֱ��������O�İ뾶Ϊ12��sinB=$\frac{1}{4}$�����߶�AC�ij����ǣ�������| A�� | 6 | B�� | 5 | C�� | 4 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
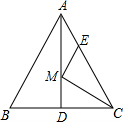 ��ͼ���ȱߡ�ABC�ı߳�Ϊ6��AD��BC���ϵ����ߣ�M��AD�ϵĶ��㣬E�DZ�AC��һ�㣬��AE=2����EM+CM����СֵΪ��������
��ͼ���ȱߡ�ABC�ı߳�Ϊ6��AD��BC���ϵ����ߣ�M��AD�ϵĶ��㣬E�DZ�AC��һ�㣬��AE=2����EM+CM����СֵΪ��������| A�� | $\sqrt{26}$ | B�� | 3$\sqrt{3}$ | C�� | 2$\sqrt{7}$ | D�� | 4$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
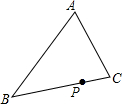 ��ͼ����P�ڡ�ABC�DZ���һ���㣬�����ҵ�һ������P��ֱ�ߣ��ѡ�ABC�ֳ������ȵ������֣���ͼ�л�������ֱ�߲�����������ȡAB�е�D������D��DE��AP��AB�ڵ�E����AD���H������EP����Ϊ����
��ͼ����P�ڡ�ABC�DZ���һ���㣬�����ҵ�һ������P��ֱ�ߣ��ѡ�ABC�ֳ������ȵ������֣���ͼ�л�������ֱ�߲�����������ȡAB�е�D������D��DE��AP��AB�ڵ�E����AD���H������EP����Ϊ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
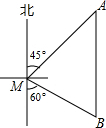 ��ͼ��һ���洬λ��С��M�ı�ƫ��45�㷽����С��180�����A�����洬��A�������Ϸ�����һ�ξ������λ��С����ƫ��60�㷽���B�������洬��A��B�ĺ��й�������С��M֮�����С���룮������ø��ű�ʾ��
��ͼ��һ���洬λ��С��M�ı�ƫ��45�㷽����С��180�����A�����洬��A�������Ϸ�����һ�ξ������λ��С����ƫ��60�㷽���B�������洬��A��B�ĺ��й�������С��M֮�����С���룮������ø��ű�ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 40 | B�� | 48 | C�� | 50 | D�� | 100 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com