
分析 (1)根据“在三角形中任意两边之和大于第三边,任意两边之差小于第三边”,结合因式分解进行证明原式为负数.
(2)先把原式化为完全平方的形式,再利用非负数的性质求解.
解答 解:(1)∵a、b、c分别为△ABC的三边,
∴a+b>c,b+c>a,
即a-c+b>0,a-c-b<0.
∴(a-c)2-b2=(a-c+b)(a-c-b)<0
∴(a-c)2-b2是负数.
(2)∵a2+c2+2b(b-a-c)=0,
∴a2+c2-2ab-2bc+2b2=0,
a2+b2-2ab+c2-2bc+b2=0,
即(a-b)2+(b-c)2=0,
∴a-b=0且b-c=0,即a=b且b=c,
∴a=b=c.
故△ABC是等边三角形.
点评 本题主要考查了因式分解的应用和非负数的性质,利用了平方差公式和三角形三边的关系进行分析(1)题,利用完全平方公式因式分解是解答(2)题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
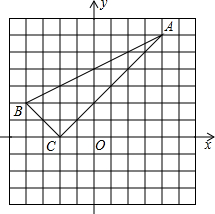 如图,已知△ABC的三个顶点的坐标分别为A(4,6),B(-4,2),C(-2,0).
如图,已知△ABC的三个顶点的坐标分别为A(4,6),B(-4,2),C(-2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
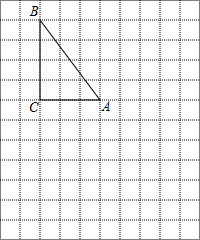 在下列网格中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4,
在下列网格中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
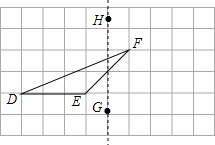 如图,在正方形网格上有一个△DEF.
如图,在正方形网格上有一个△DEF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | S=x(20-x) | B. | S=x(20-2x) | C. | S=10x-x2 | D. | S=2x(10-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
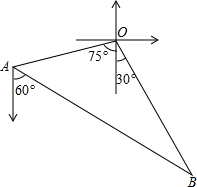 如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?
如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时15海里的速度航行,甲沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.甲船追赶乙船的速度为多少海里/小时?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
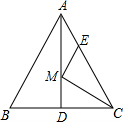 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是边AC上一点,若AE=2,则EM+CM的最小值为( )| A. | $\sqrt{26}$ | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{7}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com