
【题目】已知函数![]()
(1)m= 时,函数图像与x轴只有一个交点;
(2)m为何值时,函数图像与x轴没有交点;
(3)若函数图像与x轴交于A、B两点,与y轴交于点C,且△ABC的面积为4,求m的值.
【答案】(1) ![]() 或
或![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)分两种情况进行讨论:①当m-1=0时,函数是一次函数,图象是直线,与x轴有一个交点;②当m-1≠0时,函数是二次函数,令根的判别式等于0,求出m的值,即可得到结果;
(2)令根的判别式小于0即可求出m的范围;
(3)对于二次函数解析式,分别令x与y为0求出y与x的值,利用根与系数的关系求出两个之和与两根之积,表示出三角形ABC的面积,根据已知面积为4即可求出m的值.
试题解析:
解:(1)分两种情况进行讨论:
①当m-1=0,m=1时,函数是一次函数y=2x,图象是直线,与x轴有一个交点;
②当m-1≠0,m≠1时,函数是二次函数,
∵函数y=(m-1)x2+2mx+m-1图象与x轴只有一个交点,
∴△=4m2-4(m-1)2=4m2-4m2+8m-4=0,
解得:m=![]() .
.
故答案为1或![]() ;
;
(2)∵函数与x轴没有交点,
∴△=4m2-4(m-1)2=4m2-4m2+8m-4<0,即m<![]() ;
;
(3)对于二次函y=(m-1)x2+2mx+m-1,
令x=0,得到y=m-1,即C(0,m-1),
令y=0,得到(m-1)x2+2mx+m-1=0,
设此方程的两根为a,b,
∴由根与系数的关系得到a+b=![]() , ab=1,
, ab=1,
∴AB=|a-b|=![]() =
=![]() =
= ,
,
∵△ABC的面积为4,
∴![]() AByC纵坐标=4,即|m-1|×
AByC纵坐标=4,即|m-1|×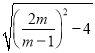 =8,
=8,
两边平方得:4m2-4(m-1)2=64,即8m=68,
解得:m=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.
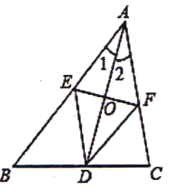
(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若DE=13,EF=10,求AD的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
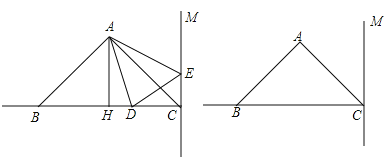
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用了随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 .
(2)请补全条形统计图.
(3)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用画树状图或列表的方法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
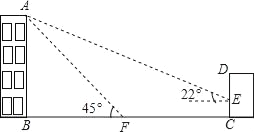
【题目】如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上)
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com