
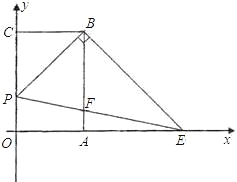
【题目】如图,已知矩形OABC,以点O为坐标原点建立平面直角坐标系,其中A(2,0),C(0,3),点P以每秒1个单位的速度从点C出发在射线CO上运动,连接BP,作BE⊥PB交x轴于点E,连接PE交AB于点F,设运动时间为t秒.
(1)当t=2时,求点E的坐标;
(2)若AB平分∠EBP时,求t的值.
(3)在运动的过程中,是否存在以P、O、E为顶点的三角形与△ABE相似.若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)E(5,0);(2)∴t=2;(3)存在;(0,![]() )或(0,
)或(0,![]() ).
).
【解析】
(1)本题需先求出AB=AE,再求出DE=5,即可求出点E的坐标.
(2)本题需先求出CP=CB=2,即可求出t的值.
(3)本题需先证出△BCP∽△BAE,求出AE=![]() t,再分两种情形分别求解即可解决问题;
t,再分两种情形分别求解即可解决问题;
解:(1)当t=2时,PC=2,
∵BC=2,
∴PC=BC,
∴∠PBC=45°,
∴∠BAE=90°,
∴∠AEB=45°,
∴AB=AE=3,
∴OE=5,
∴点E的坐标是(5,0);
(2)当AB平分∠EBP时,
∠PBF=45°,
则∠CBP=∠CPB=45°,
∴CP=CB=2,
∴t=2;
(3)存在,
∵∠ABE+∠ABP=90°,
∠PBC+∠ABP=90°,
∴∠ABE=∠PBC,
∵∠BAE=∠BCP=90°,
∴△BCP∽△BAE,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() t,
t,
∵若△POE∽△EAB,
∴![]() ,
,
∴ ,
,
∴t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
∴P的坐标为(0,![]() );
);
当点P在y轴的负半轴上时,若△POE∽△EAB,则有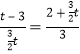 ,无解,
,无解,
若△POE∽△BAE,则有: ,
,
解得t=3+![]() 或3﹣
或3﹣![]() (舍弃)
(舍弃)
∴P的坐标为(0,![]() )或(0,
)或(0,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
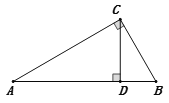
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于D,△BCD的周长为(6+2![]() )cm,则△ABC的周长为( )cm.
)cm,则△ABC的周长为( )cm.
A.(9+2![]() )B.(12+
)B.(12+![]() )C.(12+4
)C.(12+4![]() )D.(18+2
)D.(18+2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知:如图1,在Rt△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,∠C=∠C′=90°.求证:Rt△ABC和Rt△A′B′C′全等.
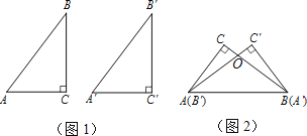
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)如图2,将△ABC和A′B′C′拼在一起(即:点A与点B′重合,点B与点A′重合),BC和B′C′相交于点O,请用此图证明上述命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有360米;其中正确的结论有( )
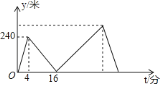
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
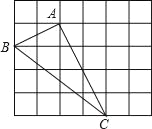
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为 ,CD的长为 ,AD的长为_____;
(3)△ACD为 三角形,四边形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=![]() x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com