
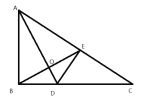
【题目】如图,将△ABC沿直线AD折叠,点B与点E重合,连接BE交AD于O.∠ABC=90°,AB=6,BC=8,AC=10,SACD=15.有下列结论:①SCDE=5;②CD=5;③OB=OE;④SABD:SACD=3:4,则以上结论正确的是( )
A. ①②B. ②③C. ②③④D. ①②③
【答案】B
【解析】
由题意可得△ABD≌△AED,∠AED=∠ABC=90°,AE=AB=6,则CE=4,由SACD=15可得DE=3,即可求得SCDE; 由BD= DE=3,可得CD=BC-BD=5;由△ABD≌△AED得∠BAD=∠CAD,AB=AE,由等腰三角形三线合一可得OB=OE;由SABD=![]() ,可得SABD:SACD=9:15=3:5.
,可得SABD:SACD=9:15=3:5.
解: ∵△ABC沿直线AD折叠,点B与点E重合,
∴△ABD≌△AED,
∴∠AED=∠ABC=90°,AE=AB=6,BD= DE,
∵SACD=![]() =15,AC=10,
=15,AC=10,
∴BD= DE=3,CE=AC-AE=4,
∴SCDE =![]() ,故①错误;
,故①错误;
∵△ABD≌△AED,
∴BD= DE=3,
∴CD=BC-BD=8-3=5,故②正确;
∵△ABD≌△AED,
∴∠BAD=∠CAD,AB=AE,
∴OB=OE,故③正确;
∵SABD=![]() ,SACD=15,
,SACD=15,
∴SABD:SACD=9:15=3:5,故④错误.
故以上结论正确的是②③.
故选B.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 为平面内一点,
为平面内一点,![]() 于
于![]() .
.
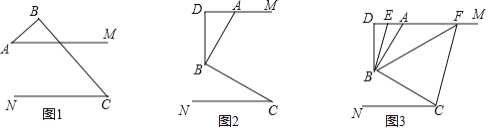
(1)如图1,直接写出![]() 和
和![]() 之间的数量关系 ;
之间的数量关系 ;
(2)如图2,过点![]() 作
作![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)问的条件下,点![]() 、
、![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】延庆区由于生态质量良好、自然资源丰富,成为北京的生态涵养区,是其生态屏障和水源保护地.为降低空气污染,919公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,在下列说法中:
①ac<0;
②方程ax2+bx+c=0的根是x1=﹣1,x2=3;
③a+b+c>0;
④当x>1时,y随着x的增大而增大.
正确的说法有 . (请写出所有正确的序号)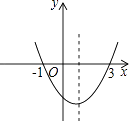
查看答案和解析>>
科目:初中数学 来源: 题型:
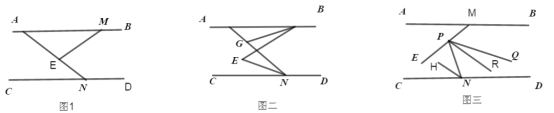
【题目】(1)如图1,![]() ,
,![]() 分别在
分别在![]() 上,试说明∠MEN=∠INC+∠IME.
上,试说明∠MEN=∠INC+∠IME.
(2)如图2,在(1)的条件下,若![]() 平分
平分![]() ,在
,在![]() 上有一点
上有一点![]() ,连接
,连接![]() ,使
,使![]() 恰好平分
恰好平分![]() ,
,![]() ,且
,且![]() 的补角比
的补角比![]() 的3倍多
的3倍多![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,在问题(1)(2)的条件下,若点![]() 是
是![]() 上一动点(不包含点
上一动点(不包含点![]() 和点
和点![]() ),连接
),连接![]() .
.![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,过
,过![]() 作
作![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时,下列结论:①
上运动时,下列结论:①![]() 的值不变;②
的值不变;②![]() 的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
的度数不变,可以证明只有一个是正确的,请你做出正确选择并求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:长方形ABCD在坐标平面内的位置如图所示, A(1,1) C(-3,-4),点P从点A出发,沿着A→B→C→D→A的路径,以每秒![]() 个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.
个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.
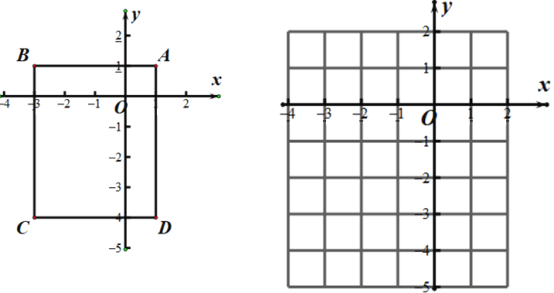
(1)直接写出点B、点D的坐标.
(2)当t=6秒时,写出P点的坐标.
(3)当点P运动到与x轴的距离为![]() 个单位时直接写出t的值.
个单位时直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①![]() BCD≌
BCD≌![]() CBE;②
CBE;②![]() BAD≌
BAD≌![]() BCD;③
BCD;③![]() BDA≌
BDA≌![]() CEA;④
CEA;④![]() BOE≌
BOE≌![]() COD;⑤
COD;⑤ ![]() ACE≌
ACE≌![]() BCE;上述结论一定正确的是
BCE;上述结论一定正确的是
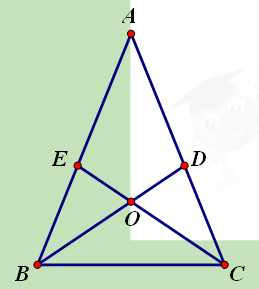
A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com