
【题目】延庆区由于生态质量良好、自然资源丰富,成为北京的生态涵养区,是其生态屏障和水源保护地.为降低空气污染,919公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
【答案】
(1)解:由题意得: ![]() ,
,
解这个方程组得: ![]() .
.
答:购买A型公交车每辆需100万元,购买B型公交车每辆需150万元.
(2)解:设购买A型公交车x辆,购买B型公交车(10﹣x)辆,
由题意得: ![]() ,
,
解得:6≤x≤8,
有三种购车方案:①购买A型公交车6辆,购买B型公交车4辆;
②购买A型公交车7辆,购买B型公交车3辆;
③购买A型公交车8辆,购买B型公交车2辆.
故购买A型公交车越多越省钱,
所以购车总费用最少的是购买A型公交车8辆,购买B型公交车2辆.
【解析】(1)由“A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元”构建方程组由题意得:![]() 解方程组,可得出答案;(2)由“A型和B型公交车的总费用不超过1200万元客总和不少于680万人次”构建不等式组
解方程组,可得出答案;(2)由“A型和B型公交车的总费用不超过1200万元客总和不少于680万人次”构建不等式组![]() ,解不等式组,求整数解,找出最省钱方案.
,解不等式组,求整数解,找出最省钱方案.
【考点精析】解答此题的关键在于理解一元一次不等式组的应用的相关知识,掌握1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.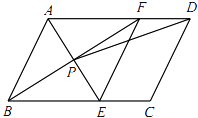
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39②,②一①得:3S﹣S=39﹣1,即2S=39﹣1,∴S= ![]() .得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 .
.得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式.例如,分式是![]() ,
,![]() 是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式
是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式![]() ,
,![]() 是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,
是假分式.一个假分式可以化为一个整式与一个真分式的和.例如,![]() =
=![]() =1-
=1-![]() .
.
(1)将假分式![]() 化为一个整式与一个真分式的和;
化为一个整式与一个真分式的和;
(2)如果分式![]() 的值为整数,求x的整数值.
的值为整数,求x的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
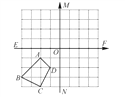
【题目】(齐齐哈尔中考)如图所示,在四边形ABCD中.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称,若对称请在图中画出对称轴或对称中心.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )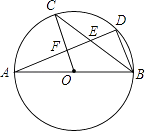
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿直线AD折叠,点B与点E重合,连接BE交AD于O.∠ABC=90°,AB=6,BC=8,AC=10,SACD=15.有下列结论:①SCDE=5;②CD=5;③OB=OE;④SABD:SACD=3:4,则以上结论正确的是( )
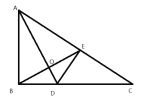
A. ①②B. ②③C. ②③④D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.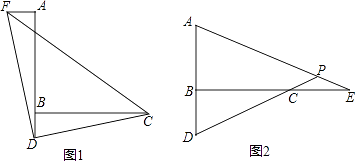
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com