
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.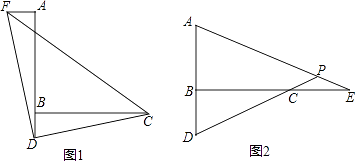
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
【答案】
(1)解:△CDF是等腰直角三角形,理由如下:
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
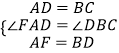 ,
,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形;
(2)解:作AF⊥AB于A,使AF=BD,连结DF,CF,如图,
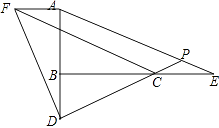
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
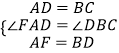 ,
,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,
∴∠FCD=45°,
∵AF∥CE,且AF=CE,
∴四边形AFCE是平行四边形,
∴AE∥CF,
∴∠APD=∠FCD=45°.
【解析】(1)利用SAS证出△FAD≌△DBC,再利用全等三角形的性质得出FD=DC,∠FDA=∠DCB,故△CDF是等腰直角三角形;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,如图,利用SAS证明△FAD≌△DBC,再利用全等三角形的性质得出FD=DC,![]() FDC=90°.故△CDF是等腰直角三角形,从而推出∠FCD=45°,由AF∥CE,且AF=CE,推出四边形AFCE是平行四边形,根据平行四边形的性质得出AE∥CF,根据平行线的性质得出结论。
FDC=90°.故△CDF是等腰直角三角形,从而推出∠FCD=45°,由AF∥CE,且AF=CE,推出四边形AFCE是平行四边形,根据平行四边形的性质得出AE∥CF,根据平行线的性质得出结论。
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等,以及对平行四边形的判定与性质的理解,了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】延庆区由于生态质量良好、自然资源丰富,成为北京的生态涵养区,是其生态屏障和水源保护地.为降低空气污染,919公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年载客量如表:
A型 | B型 | |
价格(万元/台) | a | b |
年载客量(万人/年) | 60 | 100 |
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求a,b的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:长方形ABCD在坐标平面内的位置如图所示, A(1,1) C(-3,-4),点P从点A出发,沿着A→B→C→D→A的路径,以每秒![]() 个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.
个单位的速度运动.运动一周回到A点时停止运动.设运动时间为t秒.
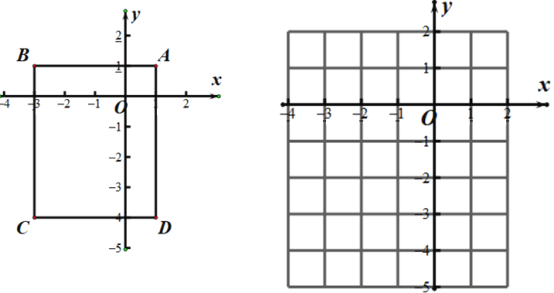
(1)直接写出点B、点D的坐标.
(2)当t=6秒时,写出P点的坐标.
(3)当点P运动到与x轴的距离为![]() 个单位时直接写出t的值.
个单位时直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在△ABC中,AB=AC,点D是线段BC上一个动点,以AD为腰在线段AD的右侧作△ADE,且AD=AE。
(1)如图①,当∠BAC=∠DAE=90°时,试判断线段BD和CE有什么关系,并给出证明:
(2)在(1)的条件下,若BC=4.试判断四边形ADCE的面积是否发生变化,若不变,求出四边形ADCE的面积;若变化,请说明理由;
(3)如图②,若∠BAC=∠DAE=120°,BC=4,试探索△DCE的面积是否存在最大值,若存在,求出此时∠DEC的度数,若不存在,请说明理由。
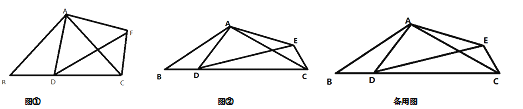
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①![]() BCD≌
BCD≌![]() CBE;②
CBE;②![]() BAD≌
BAD≌![]() BCD;③
BCD;③![]() BDA≌
BDA≌![]() CEA;④
CEA;④![]() BOE≌
BOE≌![]() COD;⑤
COD;⑤ ![]() ACE≌
ACE≌![]() BCE;上述结论一定正确的是
BCE;上述结论一定正确的是
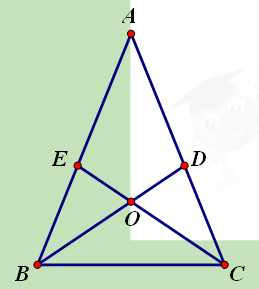
A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程x2+mx+n=0有两个不相等实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com