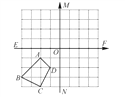
【题目】(齐齐哈尔中考)如图所示，在四边形ABCD中.
(1)画出四边形A1B1C1D1，使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称；
(2)画出四边形A2B2C2D2，使四边形A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称，若对称请在图中画出对称轴或对称中心.
【答案】答案见解析.
【解析】试题分析：(1)使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称则过A、B、C、D分别作MN的垂线段，并延长使A1、B1、C1、D1到MN的距离等于A、B、C、D到MN的距离.再顺次连接A1、B1、C1、D1即可.(2)过A、B、C、D作射线AO、BO、CO、DO，在射线上分别取OA1=OA、OB1=OB、OC1=OC、OD1=OD，再顺次连接A1、B1、C1、D1即可.（3）四边形A1B1C1D1与四边形A2B2C2D2对称，连接对称点作垂直平分线会发现对称轴为图形中的直线EF.
(1)
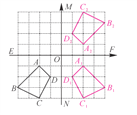
(2)如图所示；
(3)四边形A1B1C1D1与四边形A2B2C2D2对称，对称轴为图形中的直线EF
全能测控期末小状元系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AD平分∠BAC，
(1)图①中，已知AF⊥BC , ∠B=500，∠C=600. 求∠DAF的度数.
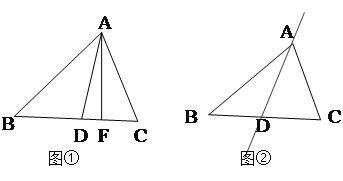
（2）图②中，请你在直线AD上任意取一点E（不与点A、D重合），画EF⊥BC，垂足为F.已知∠B=α，∠C=β（β＞a）.求∠DEF的度数. （用α、β的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC=∠BEF=60°，则 
=（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为
的大正方形，两块是边长都为
的小正方形，五块是长为，宽为的全等小矩形，且
．（以上长度单位：
）
（1）观察图形，发现代数式
可以因式分解为_________________；
（2）若每块小矩形的面积为
，四个正方形的面积和为
，试求图中所有裁剪线（虚线部分）的长度之和．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】延庆区由于生态质量良好、自然资源丰富，成为北京的生态涵养区，是其生态屏障和水源保护地．为降低空气污染，919公交公司决定全部更换节能环保的燃气公交车．计划购买A型和B型两种公交车共10辆，其中每台的价格，年载客量如表：
A型 | B型 | |
价格（万元/台） | a | b |
年载客量（万人/年） | 60 | 100 |
若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求a，b的值；
（2）如果该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次．请你设计一个方案，使得购车总费用最少．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AC，BD为对角线，AB＝BC＝AC＝BD，则∠ADC的大小为( )
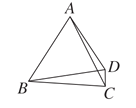
A. 120°B. 135°C. 145°D. 150°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图为二次函数y=ax2+bx+c的图象，在下列说法中：
①ac＜0；
②方程ax2+bx+c=0的根是x1=﹣1，x2=3；
③a+b+c＞0；
④当x＞1时，y随着x的增大而增大．
正确的说法有 ． （请写出所有正确的序号）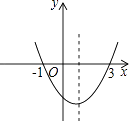
查看答案和解析>>
科目：初中数学 来源： 题型：
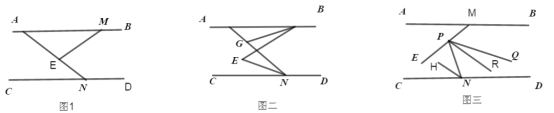
【题目】（1）如图1，
，
分别在
上，试说明∠MEN=∠INC+∠IME．
（2）如图2，在（1）的条件下，若
平分
，在
上有一点
，连接
，使
恰好平分
，
，且
的补角比
的3倍多
，求的度数；
（3）如图3，在问题（1）（2）的条件下，若点
是
上一动点(不包含点
和点
)，连接
．
平分
，
平分
，过作
，当点在线段上运动时，下列结论：①
的值不变；②
的度数不变，可以证明只有一个是正确的，请你做出正确选择并求值．
查看答案和解析>>
科目：初中数学 来源： 题型：
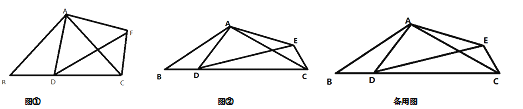
【题目】已知如图,在△ABC中,AB=AC,点D是线段BC上一个动点,以AD为腰在线段AD的右侧作△ADE,且AD=AE。
(1)如图①,当∠BAC=∠DAE=90°时,试判断线段BD和CE有什么关系,并给出证明:
(2)在(1)的条件下,若BC=4.试判断四边形ADCE的面积是否发生变化,若不变,求出四边形ADCE的面积;若变化,请说明理由;
(3)如图②,若∠BAC=∠DAE=120°,BC=4,试探索△DCE的面积是否存在最大值,若存在,求出此时∠DEC的度数,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com