
【题目】如图,△ABC中,AD平分∠BAC,
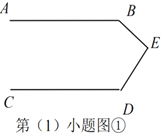
(1)图①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度数.
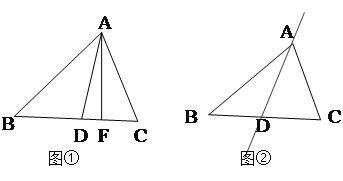
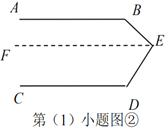
(2)图②中,请你在直线AD上任意取一点E(不与点A、D重合),画EF⊥BC,垂足为F.已知∠B=α,∠C=β(β>a).求∠DEF的度数. (用α、β的代数式表示)
【答案】(1)∠DAF=5°(2)∠DEF=![]() (β-α)
(β-α)
【解析】试题分析:根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由垂直的定义可得∠AFC的度数,根据直角三角形的两锐角互余即可求得∠DAF的度数;(2)如图2,根据三角形的内角和定理可求得∠BAC的度数,又因AD平分∠BAC,根据角平分线的定义可求得∠CAD的度数,再由三角形的内角和定理求得∠ADC的度数,再由垂直的定义可得∠EFD的度数,根据直角三角形的两锐角互余即可求得∠DEF的度数;如图3,类比图2的方法解决问题即可.
试题解析:
(1)∵∠B=500,∠C=600,
∴∠BAC=180°-∠B-∠C=180°-500-600 =70°,
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() ×70°=35°,
×70°=35°,
又∵AF⊥BC ,
∴∠AFC =90°,
∴∠CAF =90° -∠C =30°,
∴ ∠DAF =∠CAD -∠CAF =5°.
(2)① 如图,

图2
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠ADC =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).
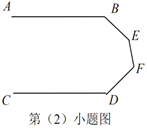
②如图,
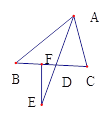
图3
∵∠B=α,∠C=β,
∴∠BAC=180°-∠B-∠C=180°-(α+β),
∵AD平分∠BAC,
∴∠CAD = ![]() ∠BAC =
∠BAC =![]() [180°-(α+β)]=90°-
[180°-(α+β)]=90°-![]() (α+β),
(α+β),
∴∠ADC=180°-∠CAD-∠C=180°-[90°-![]() (α+β)]- β=90°+
(α+β)]- β=90°+![]() α-
α-![]() β
β
∴∠ADC=∠EDF=90°+![]() α-
α-![]() β,
β,
又∵EF⊥BC ,
∴∠EFD=90°,
∴∠DEF =90° -∠EDF =90°-[90°+![]() α-
α-![]() β]=
β]= ![]() (β-α).
(β-α).


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】为了让更多的居民享受免费的体育健身服务,重庆市将陆续建成多个社区健身点,某社区为了了解健身点的使用情况,现随机调查了部分社区居民,将调查结果分成四类,A:每天健身;B:经常健身;C:偶尔健身;D:从不健身;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图,解答下列问题: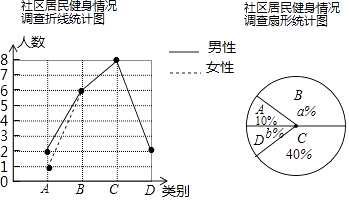
(1)本次调查中,一共调查了名社区居民,其中a=;请将折线统计图补充完整;
(2)为了吸引更多社区居民参加健身,健身点准备举办一次健身讲座培训,为此,想从被调查的A类和D类居民中分别选取一位在讲座上进行交流,请用列表法或画树状图的方法列出所有等可能的结果,并求出所选两位居民恰好是一位男性和一位女性的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
汽车运费(元/辆) |
|
|
|
(1)若全部物资都用甲、乙两种车型来运送,需运费![]() 元,问分别需甲、乙两种车型各几辆?
元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知他们的总辆数为![]() 辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.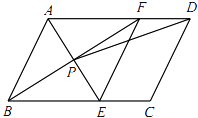
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
(1)如图①,已知![]() ,试探究直线
,试探究直线![]() 与
与![]() 有怎样的位置关系?并说明理由.
有怎样的位置关系?并说明理由.
小明给出下面正确的解法:
直线![]() 与
与![]() 的位置关系是
的位置关系是![]() .
.
理由如下:
过点![]() 作
作![]() (如图②所示)
(如图②所示)
所以![]() (依据1)
(依据1)
因为![]() (已知)
(已知)
所以![]()
所以![]()
所以![]() (依据2)
(依据2)
因为![]()
所以![]() (依据3)
(依据3)
交流反思
上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?
“依据1”:________________________________;
“依据2”:________________________________;
“依据3”:________________________________.
类比探究
(2)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件________时,有
满足条件________时,有![]() .
.
拓展延伸
(3)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件_________时,有
满足条件_________时,有![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数1至2018按一定规律排列如下表:
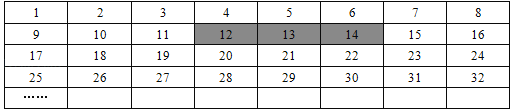
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2019 B. 2018 C. 2016 D. 2013
查看答案和解析>>
科目:初中数学 来源: 题型:
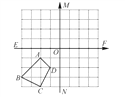
【题目】(齐齐哈尔中考)如图所示,在四边形ABCD中.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称,若对称请在图中画出对称轴或对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com