
【题目】问题情境
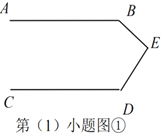
(1)如图①,已知![]() ,试探究直线
,试探究直线![]() 与
与![]() 有怎样的位置关系?并说明理由.
有怎样的位置关系?并说明理由.
小明给出下面正确的解法:
直线![]() 与
与![]() 的位置关系是
的位置关系是![]() .
.
理由如下:
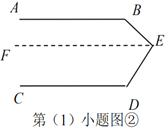
过点![]() 作
作![]() (如图②所示)
(如图②所示)
所以![]() (依据1)
(依据1)
因为![]() (已知)
(已知)
所以![]()
所以![]()
所以![]() (依据2)
(依据2)
因为![]()
所以![]() (依据3)
(依据3)
交流反思
上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?
“依据1”:________________________________;
“依据2”:________________________________;
“依据3”:________________________________.
类比探究
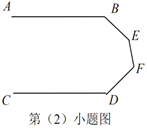
(2)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件________时,有
满足条件________时,有![]() .
.
拓展延伸
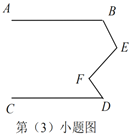
(3)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件_________时,有
满足条件_________时,有![]() .
.
【答案】(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;(2)∠B+∠E+∠F+∠D=540°;(3)∠B+∠E+∠D-∠F=180°.
【解析】
(1)根据平行线的性质和判定,平行公理的推论回答即可;
(2)过点E、F分别作GE∥HF∥CD,根据两直线平行,同旁内角互补及已知条件求得同旁内角∠ABE+∠BEG=180°,得到AB∥GE,再根据平行线的传递性来证得AB∥CD;
(3)过点E、F分别作ME∥FN∥CD,根据两直线平行,内错角相等及已知条件求得同旁内角∠B+∠BEM=180°,得到AB∥ME,再根据平行线的传递性来证得AB∥CD.
解:(1)由题意可知:“依据1”:两直线平行,同旁内角互补;
“依据2”: 同旁内角互补,两直线平行;
“依据3”: 如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.
理由:如图,过点E、F分别作GE∥HF∥CD,
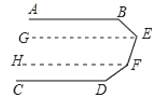
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠BEF+∠EFD+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
(3)当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠D-∠F=180°时,有AB∥CD.
如图,过点E、F分别作ME∥FN∥CD,
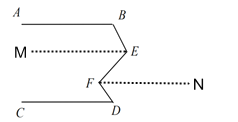
则∠MEF=EFN,∠D=∠DFN,
∵∠B+∠BEF+∠D-∠EFD=180°,
∴∠B+∠BEM+∠MEF+∠D-∠EFN-∠DFN=180°,
∴∠B+∠BEM=180°,
∴AB∥ME,
∴AB∥CD.


科目:初中数学 来源: 题型:
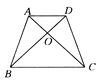
【题目】如图所示,在四边形ABCD中,已知AB与 CD不平行,∠ABD=∠ACD,请你添加一个条件:______ ,使的加上这个条件后能够推出AD∥BC ,且AB=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.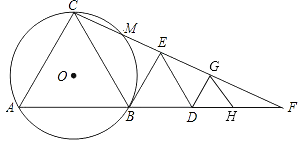
(1)求证:AC 2=CMCF;
(2)若CM= ![]() ,MF=
,MF= ![]() ,求圆O的半径长;
,求圆O的半径长;
(3)设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,
(1)图①中,已知AF⊥BC , ∠B=500,∠C=600. 求∠DAF的度数.
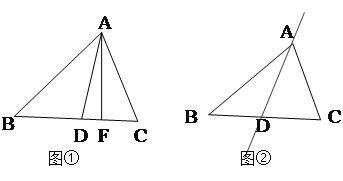
(2)图②中,请你在直线AD上任意取一点E(不与点A、D重合),画EF⊥BC,垂足为F.已知∠B=α,∠C=β(β>a).求∠DEF的度数. (用α、β的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ).
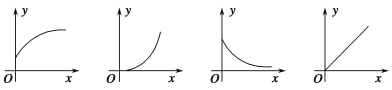
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省教育厅下发了![]() 在全省中小学幼儿园广泛开展节约教育的通知
在全省中小学幼儿园广泛开展节约教育的通知![]() ,通知中要求各学校全面持续开展“光盘行动”
,通知中要求各学校全面持续开展“光盘行动”![]() 深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度
深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度![]() 程度分为:“A:了解很多”、“B:了解较多”、“C:了解较少”、“D:不了解”
程度分为:“A:了解很多”、“B:了解较多”、“C:了解较少”、“D:不了解”![]() ,对本市某所中学的学生进行了抽样调查
,对本市某所中学的学生进行了抽样调查![]() 我们将这次调查的结果绘制了以下两幅不完整统计图:
我们将这次调查的结果绘制了以下两幅不完整统计图:
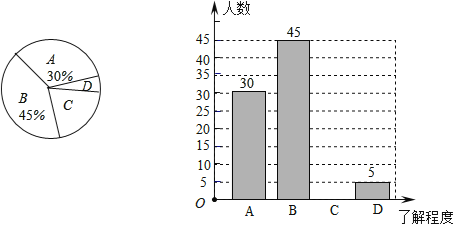
根据以上信息,解答下列问题:
![]() 补全条形统计图;
补全条形统计图;
![]() 本次抽样调查了______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
本次抽样调查了______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
![]() 若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶
点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(3),
则三角板的最大边的长为( )

A. ![]() B.
B. ![]() C.
C. ![]()
![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )
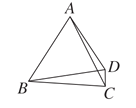
A. 120°B. 135°C. 145°D. 150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com