
【题目】如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.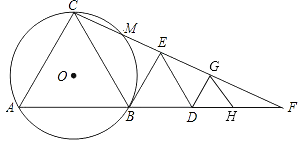
(1)求证:AC 2=CMCF;
(2)若CM= ![]() ,MF=
,MF= ![]() ,求圆O的半径长;
,求圆O的半径长;
(3)设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系.
【答案】
(1)解:连结MB,则∠CMB=180°﹣∠A=120°,
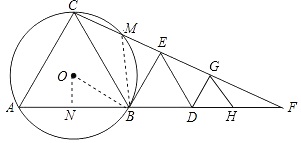
∵∠CBF=60°+60°=120°,
∴∠CMB=∠CBF,
∵∠BCM=∠FCB,
∴△CMB∽△CBF,
∴ ![]() ,即CB2=CMCF,
,即CB2=CMCF,
∵AC=CB,
∴AC2=CMCF
(2)解:过点O作ON⊥AB于点N,
则∠CMB=120°,
∵∠CBF=120°,
∴∠CMB=∠CBF,
∵∠BCF=∠BCM,
∴△CMB∽△CBF,
∴ ![]() =
= ![]() ,
,
即CB2=CMCF,
∵AC=CB=AB,CM= ![]() ,MF=
,MF= ![]() ,
,
∴CB2= ![]() ,
,
AB=AC=BC= ![]() ,
,
∵△ABC是等边三角形,
∴∠OBA=30°,
∴ON= ![]() BO,
BO,
∴cos30°= ![]() =
= ![]() =
= ![]() ,
,
解得:BO= ![]() ,
,
即⊙O的半径为: ![]() ;
;
(3)解:由题意可得:AC∥BE∥DG,BC∥DE∥HG,
∴ ![]() =
= ![]() =
= ![]()
∵ ![]() =(
=( ![]() )2
)2
![]() =(
=( ![]() )2
)2
∴ ![]() =
= ![]() 即S22=S1S3
即S22=S1S3
∴所求的数量关系是S22=S1S3.
【解析】1)连结MB易证∠CMB=∠CBF,则可以得到△CMB∽△CBF,根据相似三角形对应边的比相等即可证明;
(2)过点O作ON⊥AB于点N,易证∠CMB=∠CBF,则可以得到△CMB∽△CBF,根据相似三角形对应边的比相等即可得AB=AC=BC,从而得出△ABC是等边三角形,故∠OBA=30°,根据含30![]() 直角三角形的边之间的关系得出ON=
直角三角形的边之间的关系得出ON= ![]() BO,根据特殊锐角的三角函数值及锐角三角函数的定义列出方程求解即可;
BO,根据特殊锐角的三角函数值及锐角三角函数的定义列出方程求解即可;
(3)由题意可得:AC∥BE∥DG,BC∥DE∥HG,根据平行线分线段成比例定理及相似三角形的性质即可得出结论。
【考点精析】认真审题,首先需要了解平行线分线段成比例(三条平行线截两条直线,所得的对应线段成比例),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )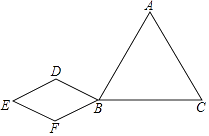
A.甲、乙都对
B.乙对甲不对
C.甲对乙不对
D.甲、乙都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为: ![]() n(n﹣3).
n(n﹣3).
如果一个n边形共有20条对角线,那么可以得到方程 ![]() .
.
整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
汽车运费(元/辆) |
|
|
|
(1)若全部物资都用甲、乙两种车型来运送,需运费![]() 元,问分别需甲、乙两种车型各几辆?
元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知他们的总辆数为![]() 辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在结束了380课时初中阶段数学内容的教学后,唐老师计划安排60课时用于总复习,根据数学内容所占课时比例,绘制如下统计图表(图1~图3),请根据图表提供的信息,回答下列问题:
(1)图1中“统计与概率”所在扇形的圆心角为度;
(2)图2、3中的a= , b=;
(3)在60课时的总复习中,唐老师应安排多少课时复习“数与代数”内容?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
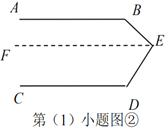
(1)如图①,已知![]() ,试探究直线
,试探究直线![]() 与
与![]() 有怎样的位置关系?并说明理由.
有怎样的位置关系?并说明理由.
小明给出下面正确的解法:
直线![]() 与
与![]() 的位置关系是
的位置关系是![]() .
.
理由如下:
过点![]() 作
作![]() (如图②所示)
(如图②所示)
所以![]() (依据1)
(依据1)
因为![]() (已知)
(已知)
所以![]()
所以![]()
所以![]() (依据2)
(依据2)
因为![]()
所以![]() (依据3)
(依据3)
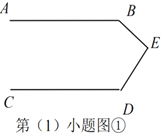
交流反思
上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?
“依据1”:________________________________;
“依据2”:________________________________;
“依据3”:________________________________.
类比探究
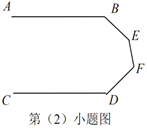
(2)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件________时,有
满足条件________时,有![]() .
.
拓展延伸
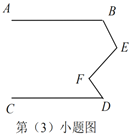
(3)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件_________时,有
满足条件_________时,有![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人在一环形场地上锻炼,甲骑自行车,乙跑步,甲比乙每分钟快200m,两人同时从起点同向出发,经过3min两人首次相遇,此时乙还需跑150m才能跑完第一圈.
![]() 求甲、乙两人的速度分别是每分钟多少米?
求甲、乙两人的速度分别是每分钟多少米?![]() 列方程或者方程组解答
列方程或者方程组解答![]()
![]() 若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过
若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过![]() 两人再次相遇,则乙的速度至少要提高每分钟多少米?
两人再次相遇,则乙的速度至少要提高每分钟多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:

(1)上表中_____是自变量,_____是因变量.
(2)你预计该地区从_____年起入学儿童的人数不超过1 000人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com