
【题目】已知点A(﹣1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可以是( )
A.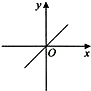
B.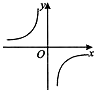
C.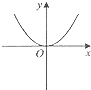
D.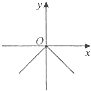
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一列数:1,2,4,8,16,…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列3,-12,48,…的第4项是______;
(2)如果一列数a1,a2,a3,a4,…是等比数列,且公比为q.那么有:a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q=a1q3,则a5=_______,an=______(用a1与q的式子表示);
(3)一个等比数列的第2项是9,第4项是36,求它的公比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )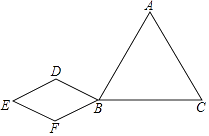
A.甲、乙都对
B.乙对甲不对
C.甲对乙不对
D.甲、乙都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并答题:我们知道,计算n边形的对角线条数公式为: ![]() n(n﹣3).
n(n﹣3).
如果一个n边形共有20条对角线,那么可以得到方程 ![]() .
.
整理得n2﹣3n﹣40=0;解得n=8或n=﹣5
∵n为大于等于3的整数,∴n=﹣5不合题意,舍去.
∴n=8,即多边形是八边形.
根据以上内容,问:
(1)若一个多边形共有14条对角线,求这个多边形的边数;
(2)A同学说:“我求得一个多边形共有10条对角线”,你认为A同学说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) |
|
|
|
汽车运费(元/辆) |
|
|
|
(1)若全部物资都用甲、乙两种车型来运送,需运费![]() 元,问分别需甲、乙两种车型各几辆?
元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知他们的总辆数为![]() 辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
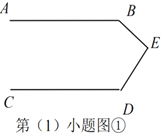
【题目】问题情境
(1)如图①,已知![]() ,试探究直线
,试探究直线![]() 与
与![]() 有怎样的位置关系?并说明理由.
有怎样的位置关系?并说明理由.
小明给出下面正确的解法:
直线![]() 与
与![]() 的位置关系是
的位置关系是![]() .
.
理由如下:
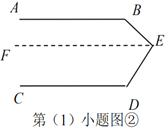
过点![]() 作
作![]() (如图②所示)
(如图②所示)
所以![]() (依据1)
(依据1)
因为![]() (已知)
(已知)
所以![]()
所以![]()
所以![]() (依据2)
(依据2)
因为![]()
所以![]() (依据3)
(依据3)
交流反思
上述解答过程中的“依据1”,“依据2”,“依据3”分别指什么?
“依据1”:________________________________;
“依据2”:________________________________;
“依据3”:________________________________.
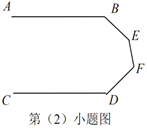
类比探究
(2)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件________时,有
满足条件________时,有![]() .
.
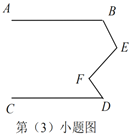
拓展延伸
(3)如图,当![]() 、
、![]() 、
、![]() 、
、![]() 满足条件_________时,有
满足条件_________时,有![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
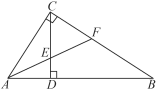
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB,交CD于点E,交BC于点F,若AF=BF,求证:△CEF是等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com