
【题目】已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.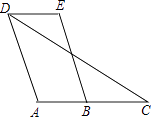
求证:∠A=∠E.
证明:∵∠EDC=∠C,
∴AB∥ . ()
∴ = . ()
∵AD∥BE,
∴∠A= . ()
∴∠A=∠E.(等量代换)
【答案】DE;内错角相等,两直线平行;∠E;∠EBC;两直线平行,内错角相等;∠EBC;两直线平行,同位角相等
【解析】证明:∵∠EDC=∠C,
∴AB∥DE(内错角相等,两直线平行),
∴∠E=∠EBC(两直线平行,内错角相等),
∵AD∥BE,
∴∠A=∠EBC(两直线平行,同位角相等),
∴∠A=∠E.(等量代换),
所以答案是:DE,内错角相等,两直线平行,∠E,∠EBC,两直线平行,内错角相等,∠EBC,两直线平行,同位角相等.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】下列各式中,计算正确的是( )
A.(15x2y﹣5xy2)÷5xy=3x﹣5y
B.98×102=(100﹣2)(100+2)=9996
C.![]()
D.(3x+1)(x﹣2)=3x2+x﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.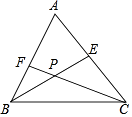
(1)若∠ABC=70°,∠ACB=50°,则∠BPC=°;
(2)求证:∠BPC=180°﹣ ![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,D、E分别为等边三角形ABC边上的点,AD=CE,BD、AE交于N,BM⊥AE于M.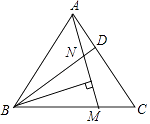
证明:
(1)∠CAE=∠ABD;
(2)MN= ![]() BN.
BN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(﹣4,2),B(﹣1,﹣2),平行四边形ABCD的对角线交于坐标原点O.
(1)请直接写出点C、D的坐标;
(2)写出从线段AB到线段CD的变换过程;
(3)直接写出平行四边形ABCD的面积.
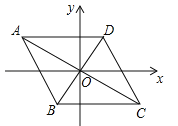
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一粒米的质量是0.000021千克,这个数字用科学记数法表示为( )
A.21×10﹣4千克
B.2.1×10﹣6千克
C.2.1×10﹣5千克
D.2.1×10﹣4千克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com