
【题目】如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点G,AD与BF相交于点H,∠BAC=50°,∠C=70°,则∠AHB= . 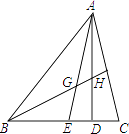
【答案】120°
【解析】解:∵在△ABC中,∠BAC=50°,∠C=70°, ∴∠ABC=60°,
∵在△ABC中,AD是高,AE,BF是角平线,
∴∠EAD=90°﹣(25°+60°)=5°,
∴∠AGH=25°+30°=55°,
∴∠AHB=180°﹣55°﹣5°=120°.
所以答案是:120°.
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内,以及对三角形的内角和外角的理解,了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧. 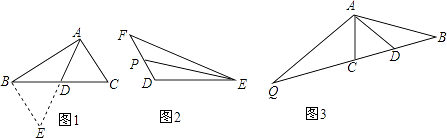
(1)【探究与发现】 如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形
(2)【理解与应用】 填空:如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是
(3)已知:如图3,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=BC,求证:AQ=2AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
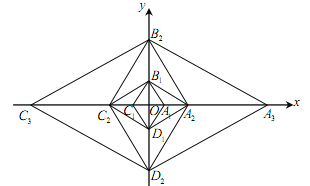
【题目】已知菱形![]() 的边长为2,
的边长为2,![]() =60°,对角线
=60°,对角线![]() ,
,![]() 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以![]() ,
,![]() 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点![]() ,
,![]() ,
,![]() ,......,
,......,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若方程ax2+bx+c=0(a≠0)中,a,b,c满足a+b+c=0和a﹣b+c=0,则方程的根是( )
A. 1,0 B. ﹣1,0 C. 1,﹣1 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=∠C,AB=16厘米,BC=12厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).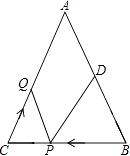
(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.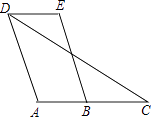
求证:∠A=∠E.
证明:∵∠EDC=∠C,
∴AB∥ . ()
∴ = . ()
∵AD∥BE,
∴∠A= . ()
∴∠A=∠E.(等量代换)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com