
【题目】八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧. 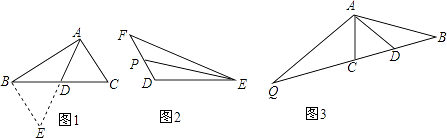
(1)【探究与发现】 如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形
(2)【理解与应用】 填空:如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是
(3)已知:如图3,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=BC,求证:AQ=2AD.
【答案】
(1)△ACD≌△EBD
(2)1<x<4
(3)证明:如图3,延长AD到M,使MD=AD,连接BM,
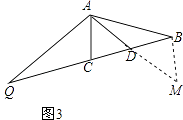
∴AM=2AD,
∵AD是△ABC的中线,
∴BD=CD,
在△BMD与△CAD中,
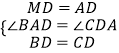 ,
,
∴△BMD≌△CAD,
∴BM=CA,∠M=∠CAD,
∴∠BAC=∠BAM+∠CAD=∠BAM+∠M,
∵∠ACB=∠Q+∠CAQ,AB=BC,
∵∠ACQ=180°﹣(∠Q+∠CAQ),∠MBA=180°﹣(∠BAM+∠M),
∴∠ACQ=∠MBA,
∵QC=BC,
∴QC=AB,
在△ACQ与△MBA中,
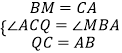 ,
,
∴△ACQ≌△MBA,
∴AQ=AM=2AD.
【解析】(1.)证明:在△ADC与△EDB中, 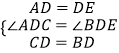 ,
,
∴△ADC≌△EDB;
所以答案是:△ADC≌△EDB;
(2.)解:如图2,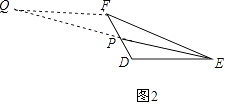
延长EP至点Q,使PQ=PE,连接FQ,
在△PDE与△PQF中,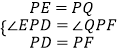 ,
,
∴△PEP≌△QFP,
∴FQ=DE=3,
在△EFQ中,EF﹣FQ<QE<EF+FQ,
即5﹣3<2x<5+3,
∴x的取值范围是1<x<4;
所以答案是:1<x<4;


科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点B,D,E在同一直线上,AF⊥BE于点F,那么线段BE,CE,AF三者之间的数量关系是 . 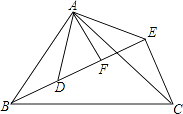
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.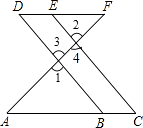
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2()
∠1=∠3()
∴∠2=∠3()
∴∥()
∴∠C=∠ABD ()
又∵∠C=∠D()
∴∠D=∠ABD()
∴AC∥DF()
查看答案和解析>>
科目:初中数学 来源: 题型:
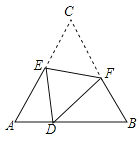
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
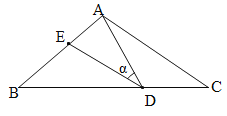
【题目】如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=![]() .有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或
.有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或![]() ;④0<BE≤
;④0<BE≤![]() ,其中正确的结论是 (填入正确结论的序号).
,其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com