
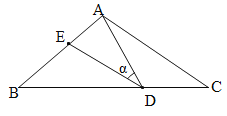
【题目】如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=![]() .有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或
.有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或![]() ;④0<BE≤
;④0<BE≤![]() ,其中正确的结论是 (填入正确结论的序号).
,其中正确的结论是 (填入正确结论的序号).
【答案】②③.
【解析】
试题分析:∵∠ADE=∠B=∠α,∠EAD=∠EAD,∴△ADE∽△ABD,而△ABD不一定相似△ACD,故①不正确;
过A作AF⊥BC于F,如图1,∵AB=AC,∴BF=FC,∵tan∠α=![]() ,∠B=∠α,∴tanB=
,∠B=∠α,∴tanB=![]() ,∴cosB=
,∴cosB=![]() ,∴
,∴![]() ,∴BF=
,∴BF=![]() AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;
AB=12,∴BC=24,∵DC=9,∴BD=BC-DC=15,∴BD=AC,∵AB=AC,∴∠B=∠C,∴∠α=∠C,∵∠C+∠CAD=∠α+∠BDE,∴∠BDE=∠CAD,在△BED和△CDA中,∵∠BDE=∠CAD,BD=AC,∠B=∠C,∴△BDE≌△CAD,故②正确;

若△BDE为直角三角形,则有两种情况:(1)若∠BED=90°,∵∠BDE=∠CAD,∠B=∠C,∴△BDE∽△CAD,∴∠CDA=∠BED=90°,∴AD⊥BC,∵AB=AC,∴BD=![]() BC=12;
BC=12;
(2)若∠BDE=90°,如图2,设BD=x,则DC=24-x,∵∠CAD=∠BDE=90°,∠B=∠C=∠α,∴cos∠C=cosB=![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴若△BDE为直角三角形,则BD为12或
,∴若△BDE为直角三角形,则BD为12或![]() ,故③正确;
,故③正确;

设BE=x,CD=y,∵△BDE∽△CAD,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴0<BE≤
,∴0<BE≤![]() ,∴故④错误;
,∴故④错误;
故答案为:②③.


科目:初中数学 来源: 题型:
【题目】如图,在长方形OABC中,O为平面直角坐标系的原点,点A坐标为(a,0),点C的坐标为(0,b),且a,b满足|a﹣4|+ ![]() =0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的线路移动.
(1)点B的坐标为 , 当点P移动3.5秒时,点P的坐标;
(2)在移动过程中,当点P到x轴的距离为4个单位长度时,求点P移动的时间;
(3)在移动过程中,当△OBP的面积是10时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧. 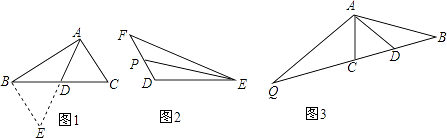
(1)【探究与发现】 如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中全等的两个三角形
(2)【理解与应用】 填空:如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是
(3)已知:如图3,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=BC,求证:AQ=2AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 ![]() 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ![]() ,则k的值是( )
,则k的值是( )
A.4
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
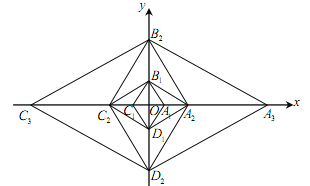
【题目】已知菱形![]() 的边长为2,
的边长为2,![]() =60°,对角线
=60°,对角线![]() ,
,![]() 相交于点O.以点O为坐标原点,分别以
相交于点O.以点O为坐标原点,分别以![]() ,
,![]() 所在直线为x轴、y轴,建立如图所示的直角坐标系.以
所在直线为x轴、y轴,建立如图所示的直角坐标系.以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,再以
,再以![]() 为对角线作菱形
为对角线作菱形![]() ∽菱形
∽菱形![]() ,,按此规律继续作下去,在x轴的正半轴上得到点
,,按此规律继续作下去,在x轴的正半轴上得到点![]() ,
,![]() ,
,![]() ,......,
,......,![]() ,则点
,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=∠C,AB=16厘米,BC=12厘米,点D为AB的中点.如果点P在线段BC上以每秒4厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).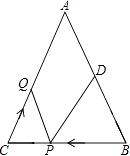
(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC≌△AEF,点F在BC上,下列结论: ①AC=AF ②∠FAB=∠EAB ③∠FAC=∠BAE ④若∠C=50°,则∠BFE=80°
其中错误结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com