
【题目】已知,D、E分别为等边三角形ABC边上的点,AD=CE,BD、AE交于N,BM⊥AE于M.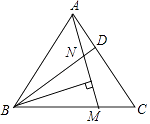
证明:
(1)∠CAE=∠ABD;
(2)MN= ![]() BN.
BN.
【答案】
(1)
证明:如图所示:
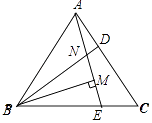
∵△ABC为等边三角形,
∴AC=AB,∠BAC=∠C=60°,
在△ABD和△CAE中, 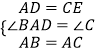 ,
,
∴△ABD≌△CAE(SAS),
∴∠CAE=∠ABD
(2)
证明:由(1)得∠CAE=∠ABD, ∵∠CAE+∠BAE=60°,
∴∠BAE+∠ABD=60°
∴∠BNM=∠BAN+∠ABN=60°,
∵BM⊥AE,
∴∠BMN=90°,
∴∠MBN=30°,
∴MN= ![]() BN.
BN.
【解析】(1)与等边三角形的性质得出AC=AB,∠BAC=∠C=60°,由SAS证明△ABD≌△CAE,得出∠CAE=∠ABD即可;
(2)由(1)得∠CAE=∠ABD,求出∠BNM=∠BAN+∠ABN=60°,得出∠BMN=90°,∠MBN=30°,由含30°角的直角三角形的性质即可得出结论.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】若方程ax2+bx+c=0(a≠0)中,a,b,c满足a+b+c=0和a﹣b+c=0,则方程的根是( )
A. 1,0 B. ﹣1,0 C. 1,﹣1 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BO平分∠ABC,CO平分∠ACB,MN过点O,交AB于M,交AC于N,且MN∥BC,若AB=12cm,AC=18cm,则△AMN周长为 . 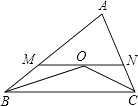
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.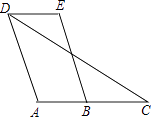
求证:∠A=∠E.
证明:∵∠EDC=∠C,
∴AB∥ . ()
∴ = . ()
∵AD∥BE,
∴∠A= . ()
∴∠A=∠E.(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Pn表示n边形的对角线的交点个数(指落在其内部的交点),如果这些交点都不重合,那么Pn与n的关系式是:Pn=![]() (其中a,b是常数,n≥4)
(其中a,b是常数,n≥4)
(1)通过画图,可得:四边形时,P4= ;五边形时,P5= ;
(2)请根据四边形和五边形对角线交点的个数,结合关系式,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】双营服装店老板到厂家选购A、B两种型号的服装,若购进A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元,
(1)求A,B两种型号的服装每件分别多少元?
(2)若销售1件A型服装可获利18元,销售1件B型服装可获利30元,根据市场需求,服装店老板决定,购进A型服装的数量要比购进B型服装数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后,可使总的获利不少于699元,问有几种进货方案如何进货?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com