
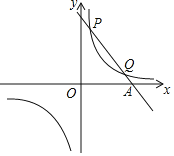
【题目】已知一次函数y=k1x+b与反比例函数y=![]() 的图象交于第一象限内的P(
的图象交于第一象限内的P(![]() ,8),Q(4,m)两点,与x轴交于A点.
,8),Q(4,m)两点,与x轴交于A点.
(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
【答案】(1) 反比例函数的表达式为y=![]() ,一次函数的表达式为y=﹣2x+9;(2) (-
,一次函数的表达式为y=﹣2x+9;(2) (-![]() ,﹣8);(3)
,﹣8);(3) ![]() .
.
【解析】
试题分析:(1)根据P(![]() ,8),可得反比例函数解析式,根据P(
,8),可得反比例函数解析式,根据P(![]() ,8),Q(4,1)两点可得一次函数解析式;
,8),Q(4,1)两点可得一次函数解析式;
(2)根据中心对称的性质,可得点P关于原点的对称点P'的坐标;
(3)过点P′作P′D⊥x轴,垂足为D,构造直角三角形,依据P'D以及AP'的长,即可得到∠P'AO的正弦值.
试题解析:(1)∵点P在反比例函数的图象上,
∴把点P(![]() ,8)代入y=
,8)代入y=![]() 可得:k2=4,
可得:k2=4,
∴反比例函数的表达式为y=![]() ,
,
∴Q (4,1).
把P(![]() ,8),Q (4,1)分别代入y=k1x+b中,
,8),Q (4,1)分别代入y=k1x+b中,
得 ,
,
解得 ,
,
∴一次函数的表达式为y=﹣2x+9;
(2)点P关于原点的对称点P'的坐标为(-![]() ,﹣8);
,﹣8);
(3)过点P′作P′D⊥x轴,垂足为D.
∵P′(-![]() ,﹣8),
,﹣8),
∴OD=![]() ,P′D=8,
,P′D=8,
∵点A在y=﹣2x+9的图象上,
∴点A(![]() ,0),即OA=
,0),即OA=![]() ,
,
∴DA=5,
∴P′A=![]() ,
,
∴sin∠P′AD=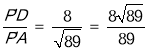 ,
,
∴sin∠P′AO= ![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
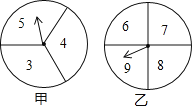
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转运甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过点A作AG∥DB交CB的延长线于点G. 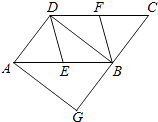
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证. 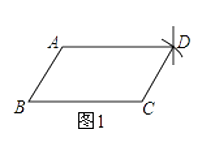
(1)已知:如图1,在四边形ABCD中,BC=AD,AB= 求证:四边形ABCD是四边形.
填空,补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
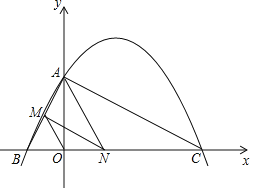
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:

根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF. 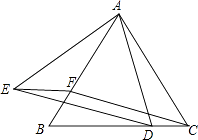
(1)求证:△ACD≌△CBF;
(2)以AD为边作等边三角形△ADE,点D在线段BC上的何处时,四边形CDEF是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com