
【题目】如图,在平面直角坐标系xOy中,已知反比例函数![]() 与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).
与一次函数y=ax+b(a≠0)的图象相交于点A(1,8)和B(4,m).
(1)分别求反比例函数和一次函数的表达式;
(2)过动点P(n,0)且垂直于x轴的直线分别与反比例函数图象和一次函数图象交于C、D两点,当点C位于点D下方时,直接写出n的取值范围.

【答案】(1)反比例函数表达式为![]() ,一次函数表达式为y=﹣2x+10;(2)n的取值范围是1<n<4.
,一次函数表达式为y=﹣2x+10;(2)n的取值范围是1<n<4.
【解析】分析:(1)把A代入反比例函数的解析式即可求得k的值,然后求得B的值,利用待定系数法即可求得一次函数的解析式;
(2)先画出两函数的图象,再根据两函数图象的上下位置关系结合交点的横坐标即可得出n的取值范围.
本题解析:
(1)∵点A(1,8)和B(4,m)在反比例函数![]() 的图象上,
的图象上,
∴k=8,m=2.
∴反比例函数表达式为![]() .
.
点B的坐标为B(4,2).
∵点A(1,8)和B(4,2)在一次函数y=ax+b的图象上,
∴![]() 解得
解得![]()
∴一次函数表达式为y=﹣2x+10;
(2)一次函数y=﹣2x+10(a≠0)的图象相交于点A(1,8)和B(4,2).
观察函数图象可知:若过动点P(n,0)且垂直于x轴的直线分别与反比例函数图象和一次函数图象交于C、D两点,当点C位于点D下方时
则n的取值范围是1<n<4.

点睛:本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征及待定系数法求函数解析式,根据两函数图象的上下位置关系找出不等式的解集是解题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠A=90°+x°,∠B=90°﹣x°,∠CED=90°,4∠C﹣∠D=30°,射线EF∥AC.
(1)判断射线EF与BD的位置关系,并说明理由;
(2)求∠C,∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划组织![]() 名师生租乘汽车外出研学一天,需租用大巴、中巴共
名师生租乘汽车外出研学一天,需租用大巴、中巴共![]() 辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐
辆,且要求租用的车子不留空位也不超载,大巴每辆可乘坐![]() 名乘客,中巴每辆可乘坐
名乘客,中巴每辆可乘坐![]() 名乘客.
名乘客.
(1)求该校应租用大巴、中巴各多少辆?(请用含![]() 的代数式表示)
的代数式表示)
(2)若每辆大巴租金是![]() 元/天,中巴租金是
元/天,中巴租金是![]() 元/天,若租金不能超过
元/天,若租金不能超过![]() 元,则应租用大巴、中巴各多少辆?
元,则应租用大巴、中巴各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC中∠ BAC的外角平分线,BD⊥AD于D,E为BC中点,DE=5,AC=3,则AB长为()

A.8.5B.8C.7.5D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=x﹣![]() 的图象和性质.
的图象和性质.
小石根据学习函数的经验,对此函数的图象和性质进行了探究.
下面是小石的探究过程,请补充完整:
(1)函数的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值,
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … | ﹣ | ﹣1 | 1 |
|
| ﹣ | ﹣ | m | 1 |
| … |
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出此函数的图象;
(4)进一步探究,结合函数的图象,写出此函数的性质(一条即可): .

查看答案和解析>>
科目:初中数学 来源: 题型:
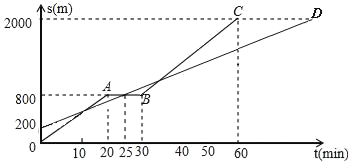
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发匀速前行,且途中休息一段时间后继续以原速前行.家到公园的距离为2000m,如图是小明和爸爸所走的路程S(m)与步行时间t(min)的函数图象.
(1)直接写出BC段图象所对应的函数关系式(不用写出t的取值范围).
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早18分钟到达公园,则小明在步行过程中停留的时间需减少 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。


(1)你认为图b中的阴影部分的正方形的边长等于__________________。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:___________________________ 方法2:___________________________
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: (m+n)2 ,(m-n)2,mn
_______________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,求(a-b)2的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com