
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( ) 
A.△AFD≌△DCE
B.AF= ![]() ?AD
?AD
C.AB=AF
D.BE=AD﹣DF
【答案】B
【解析】解:(A)由矩形ABCD,AF⊥DE可得∠C=∠AFD=90°,AD∥BC, ∴∠ADF=∠DEC.
又∵DE=AD,
∴△AFD≌△DCE(AAS),故(A)正确;
(B)∵∠ADF不一定等于30°,
∴直角三角形ADF中,AF不一定等于AD的一半,故(B)错误;
(C)由△AFD≌△DCE,可得AF=CD,
由矩形ABCD,可得AB=CD,
∴AB=AF,故(C)正确;
(D)由△AFD≌△DCE,可得CE=DF,
由矩形ABCD,可得BC=AD,
又∵BE=BC﹣EC,
∴BE=AD﹣DF,故(D)正确;
故选B.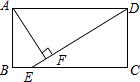
先根据已知条件判定△AFD≌△DCE(AAS),再根据矩形的对边相等,以及全等三角形的对应边相等进行判断即可.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
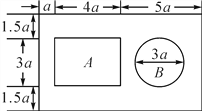
【题目】某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.(π取3.14)
(1)活动场所和花草的面积各是多少?
(2)整座健身馆的面积是成年人活动场所面积的多少倍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. x2+2x-1=(x-1)2 B. a2-a=a(a+1)
C. m2+(-n)2=(m+n)(m-n) D. -9+4y2=(3+2y)(2y-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
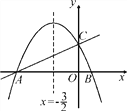
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是直线x=-![]() ,且经过A,C两点,与x轴的另一交点为点B.
,且经过A,C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线的解析式.
(2)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE
(1)填空:①∠AEB的度数为;②线段BE、AD之间的数量关系是 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com