
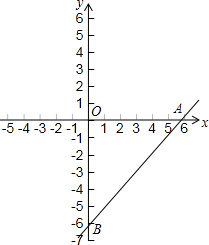 直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.
直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.分析 (1)根据轴对称的性质,可得CDEF与ABEF全等,根据全等,可得答案;
(2)根据轴对称,可得△CGF,根据三角形的面积公式,可得答案;
(3)分类讨论:当0<t≤3时,根据三角形的面积公式,可得答案;当3<t<6时,根据图形割补法,可得答案.
解答 解:(1)如图1: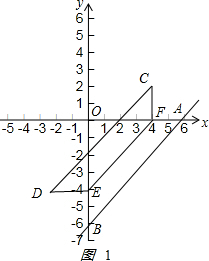
(2)如图2: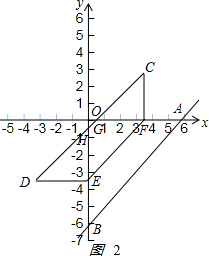 ,
,
由折叠的性质,得∠C=∠A=∠COA=45°,AF=BE=CF=t,
S△CFG=$\frac{1}{2}$CF•FG=$\frac{1}{2}$t2=$\frac{25}{8}$,
解得t=$\frac{5}{2}$,t=-$\frac{5}{2}$(不符合题意,舍);
(3)分两种情况讨论:
①当0<t≤3时,如图2: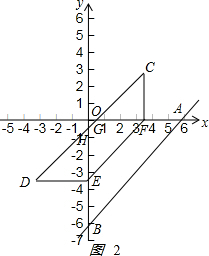
四边形DCFE落在第一象限内的图形是△DFG,
∴S=$\frac{1}{2}$t2,
∵S=$\frac{1}{2}$t2,在t>0时,S随t增大而增大,
∴t=3时,S最大=$\frac{9}{2}$;
②当3<t<6时,如图3: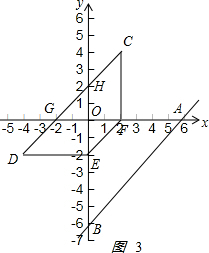 ,
,
四边形DCFE落在第一象限内的图形是四边形CHOF,
∴S四边形CHOF=S△CGF-S△HGO,
∴S=$\frac{1}{2}$t2-$\frac{1}{\;}$2(2t-6)2
=-$\frac{3}{2}$t2+12t-18
=-$\frac{3}{2}$(t-4)2+6,
∵a=-$\frac{3}{2}$<0,
∴S有最大值,
∴当t=4时,S最大=6,
综上所述,当t=4时,S最大值为6.
点评 本题考查了一次函数综合题,利用了轴对称的性质:成轴对称的两个图形全等,三角形的面积公式,图形割补法是求面积的重要方法,分类讨论是解题关键,以防遗漏.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:| 数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | d |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com