
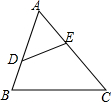
 如图,已知D,E分别是△ABC的AB,AC边上的点,且AD=5,BD=3,AE=4,CE=6,求证:∠ADE=∠C.
如图,已知D,E分别是△ABC的AB,AC边上的点,且AD=5,BD=3,AE=4,CE=6,求证:∠ADE=∠C. 分析 由条件可得$\frac{AE}{AB}=\frac{AD}{AC}$,且∠A为公共角,则可证明△ADE∽△ACB,即可得到结论.
解答 解:∵AD=5,BD=3,AE=4,CE=6,
∴AB=8,AC=10,
∴$\frac{AE}{AB}$=$\frac{4}{8}$=$\frac{1}{2}$,
$\frac{AD}{AC}$$\frac{5}{10}$=$\frac{1}{2}$,
∴$\frac{AE}{AB}=\frac{AD}{AC}$,
∵∠A=∠A,
∴△ADE∽△ACB,
∴∠ADE=∠C.
点评 本题主要考查相似三角形的判定和性质,掌握三角形相似的判定方法,即有两组角对应相等、两组对应边的比相等且夹角相等或三组对应边的比相等是解题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:选择题
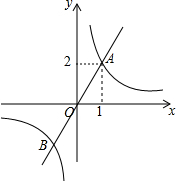 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )| A. | -1<x<0或x>1 | B. | x<-1或0<x<1 | C. | x>1 | D. | -1<x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
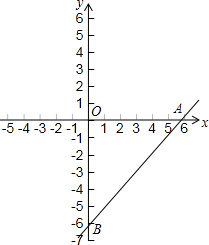 直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.
直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
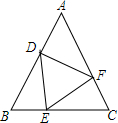 已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.
已知,如图,△ABC中,AB=AC,动点D、E、F在AB、BC、AC上移动,移动过程中始终保持BD=CE,∠DEF=∠B,请你分析是否存在始终与△BDE全等的三角形,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
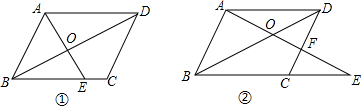 在?ABCD中,点E从点B开始沿BC方向向C点运动,如图①所示,连接AE交BD于点O,得到△AOD与△BOE始终相似.
在?ABCD中,点E从点B开始沿BC方向向C点运动,如图①所示,连接AE交BD于点O,得到△AOD与△BOE始终相似.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个三角形中可以有两个直角 | |
| B. | 一个三角形的三个内角能都大于70° | |
| C. | 一个三角形的三个内角能都小于50° | |
| D. | 三角形中最大的内角不能小于60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
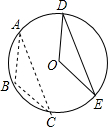 如图,△ABC是⊙O的内接三角形,平移△ABC使点B与圆心O重合,A、C两点恰好落在圆上的D、E两点处.若AC=2$\sqrt{3}$,则平移的距离为2.
如图,△ABC是⊙O的内接三角形,平移△ABC使点B与圆心O重合,A、C两点恰好落在圆上的D、E两点处.若AC=2$\sqrt{3}$,则平移的距离为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com