
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
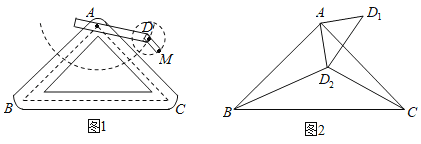
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AD=2,AB=3,点E,F分别在边AB,BC上,且BF=FC,连接DE,EF,并以DE,EF为边作DEFG.
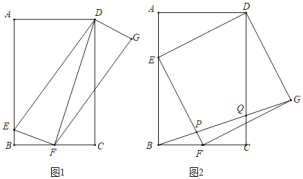
(1)连接DF,求DF的长度;
(2)求DEFG周长的最小值;
(3)当DEFG为正方形时(如图2),连接BG,分别交EF,CD于点P、Q,求BP:QG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,以AC为直径的⊙O交AB于点D,点E为弧AD的中点,连接CE交AB于点F,且BF=BC.

(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2,![]() =
=![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知
,已知![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 是
是![]() 上五点,
上五点,![]() 的直径
的直径![]() ,
,![]() .
.![]() 为
为![]() 的中点,延长
的中点,延长![]() 到点
到点![]() .使
.使![]() ,连接
,连接![]() .
.
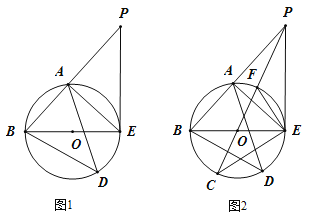
(1)求线段![]() 的长;
的长;
(2)求证:直线![]() 是
是![]() 的切线.
的切线.
(3)如图![]() ,连
,连![]() 交
交![]() 于点
于点![]() ,延长交PO交
,延长交PO交![]() 于另一点
于另一点![]() ,连
,连![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数图象是抛物线,抛物线是指平面内到一个定点![]() 和一条定直线
和一条定直线![]() 距离相等的点的轨迹.其中定点
距离相等的点的轨迹.其中定点![]() 叫抛物线的焦点,定直线
叫抛物线的焦点,定直线![]() 叫抛物线的准线.
叫抛物线的准线.
①抛物线![]() (
(![]() )的焦点为
)的焦点为![]() ,例如,抛物线
,例如,抛物线![]() 的焦点是
的焦点是![]() ;抛物线
;抛物线![]() 的焦点是___________;
的焦点是___________;
②将抛物线![]() (
(![]() )向右平移
)向右平移![]() 个单位、再向上平移
个单位、再向上平移![]() 个单位(
个单位(![]() ,
,![]() ),可得抛物线
),可得抛物线![]() ;因此抛物线
;因此抛物线![]() 的焦点是
的焦点是![]() .例如,抛物线
.例如,抛物线![]() 的焦点是
的焦点是![]() ;抛物线
;抛物线![]() 的焦点是_____________________.根据以上材料解决下列问题:
的焦点是_____________________.根据以上材料解决下列问题:
(1)完成题中的填空;
(2)已知二次函数的解析式为![]() ;
;
①求其图象的焦点![]() 的坐标;
的坐标;
②求过点![]() 且与
且与![]() 轴平行的直线与二次函数
轴平行的直线与二次函数![]() 图象交点的坐标.
图象交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃,其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃垂直于墙的一边长为x米.
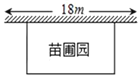
(1)若苗圃的面积为72平方米,求x的值;
(2)这个苗圃的面积能否是120平方米?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果经销商到大圩种植基地采购葡萄,经销商一次性采购葡萄的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB→BC→CD所示(不包括端点A),
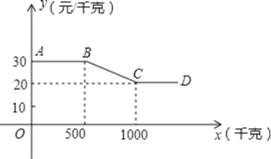
(1)当500<x≤1000时,写出y与x之间的函数关系式;
(2)葡萄的种植成本为8元/千克,某经销商一次性采购葡萄的采购量不超过1000千克,当采购量是多少时,大圩种植基地获利最大,最大利润是多少元?
(3)在(2)的条件下,若经销商一次性付了16800元货款,求大圩种植基地可以获得多少元的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
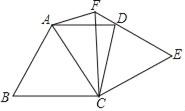
【题目】如图,将等边△ABC绕点C顺时针旋转90°得到△EFC,∠ACE的平分线CD交EF于点D,连接AD、AF.
(1)求∠CFA度数;
(2)求证:AD∥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com