
ЁОЬтФПЁПЖўДЮКЏЪ§ЭМЯѓЪЧХзЮяЯпЃЌХзЮяЯпЪЧжИЦНУцФкЕНвЛИіЖЈЕу![]() КЭвЛЬѕЖЈжБЯп
КЭвЛЬѕЖЈжБЯп![]() ОрРыЯрЕШЕФЕуЕФЙьМЃЃЎЦфжаЖЈЕу
ОрРыЯрЕШЕФЕуЕФЙьМЃЃЎЦфжаЖЈЕу![]() НаХзЮяЯпЕФНЙЕуЃЌЖЈжБЯп
НаХзЮяЯпЕФНЙЕуЃЌЖЈжБЯп![]() НаХзЮяЯпЕФзМЯпЃЎ
НаХзЮяЯпЕФзМЯпЃЎ
ЂйХзЮяЯп![]() (
(![]() )ЕФНЙЕуЮЊ
)ЕФНЙЕуЮЊ![]() ЃЌР§ШчЃЌХзЮяЯп
ЃЌР§ШчЃЌХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛХзЮяЯп
ЃЛХзЮяЯп![]() ЕФНЙЕуЪЧ___________ЃЛ
ЕФНЙЕуЪЧ___________ЃЛ
ЂкНЋХзЮяЯп![]() (
(![]() )ЯђгвЦНвЦ
)ЯђгвЦНвЦ![]() ИіЕЅЮЛЁЂдйЯђЩЯЦНвЦ
ИіЕЅЮЛЁЂдйЯђЩЯЦНвЦ![]() ИіЕЅЮЛ(
ИіЕЅЮЛ(![]() ЃЌ
ЃЌ![]() )ЃЌПЩЕУХзЮяЯп
)ЃЌПЩЕУХзЮяЯп![]() ЃЛвђДЫХзЮяЯп
ЃЛвђДЫХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЎР§ШчЃЌХзЮяЯп
ЃЎР§ШчЃЌХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛХзЮяЯп
ЃЛХзЮяЯп![]() ЕФНЙЕуЪЧ_____________________ЃЎИљОнвдЩЯВФСЯНтОіЯТСаЮЪЬтЃК
ЕФНЙЕуЪЧ_____________________ЃЎИљОнвдЩЯВФСЯНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭъГЩЬтжаЕФЬюПеЃЛ
ЃЈ2ЃЉвбжЊЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЂйЧѓЦфЭМЯѓЕФНЙЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкЧѓЙ§Еу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпгыЖўДЮКЏЪ§
жсЦНааЕФжБЯпгыЖўДЮКЏЪ§![]() ЭМЯѓНЛЕуЕФзјБъЃЎ
ЭМЯѓНЛЕуЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() КЭ
КЭ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгИљОнаТЖЈвхМДПЩЧѓГіХзЮяЯпЕФНЙЕуЃЛ
ЃЈ2ЃЉЂйЯШНЋЖўДЮКЏЪ§НтЮіЪНХфГЩЖЅЕуЪНЃЌдйИљОнаТЖЈвхМДПЩЧѓГіХзЮяЯпЕФНЙЕуЃЛ
ЂквРЬтвтПЩЕУЕу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпЃЌИљОнЦНаагкxжсЕФжБЯпЩЯЕФЕуЕФзнзјБъЯрЕШЃЌНЋЕуFЕФзнзјБъДњШыНтЮіЪНМДПЩЧѓЕУxЕФжЕЃЌДгЖјЕУГіНЛЕузјБъЃЎ
жсЦНааЕФжБЯпЃЌИљОнЦНаагкxжсЕФжБЯпЩЯЕФЕуЕФзнзјБъЯрЕШЃЌНЋЕуFЕФзнзјБъДњШыНтЮіЪНМДПЩЧѓЕУxЕФжЕЃЌДгЖјЕУГіНЛЕузјБъЃЎ
ЃЈ1ЃЉЂйИљОнаТЖЈвхЃЌПЩЕУ![]() ЃЌ
ЃЌ
ЫљвдХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛ
ЃЛ
ЂкИљОнаТЖЈвхЃЌПЩЕУh=1ЃЌ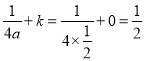 ЃЌ
ЃЌ
ЫљвдХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйНЋ![]() ЛЏЮЊЖЅЕуЪНЕУЃК
ЛЏЮЊЖЅЕуЪНЕУЃК
![]()
ИљОнаТЖЈвхЃЌПЩЕУh=1ЃЌ![]() ЃЌ
ЃЌ
ЫљвдПЩЕУХзЮяЯп![]() ЕФНЙЕузјБъ
ЕФНЙЕузјБъ![]() ЃЛ
ЃЛ
ЂкгЩЂйжЊ![]() ЃЌЫљвдЙ§Еу
ЃЌЫљвдЙ§Еу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпЪЧ
жсЦНааЕФжБЯпЪЧ![]() ЃЌ
ЃЌ
НЋ![]() ДњШы
ДњШы![]() ЕУЃК
ЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЫљвдЃЌЙ§Еу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпгыЖўДЮКЏЪ§
жсЦНааЕФжБЯпгыЖўДЮКЏЪ§![]() ЭМЯѓНЛЕуЕФзјБъЮЊ
ЭМЯѓНЛЕуЕФзјБъЮЊ![]() КЭ
КЭ![]() ЃЎ
ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФДќзгжаЃЌзАгаГ§беЩЋЭтЖМЭъШЋЯрЭЌЕФ4ИіКьЧђКЭШєИЩИіЛЦЧђЃЎ
![]() ШчЙћДгДќжаШЮвтУўГівЛИіЧђЪЧКьЧђЕФИХТЪЮЊ
ШчЙћДгДќжаШЮвтУўГівЛИіЧђЪЧКьЧђЕФИХТЪЮЊ![]() ЃЌФЧУДДќжагаЛЦЧђЖрЩйИіЃП
ЃЌФЧУДДќжагаЛЦЧђЖрЩйИіЃП
![]() дк
дк![]() ЕФЬѕМўЯТШчЙћДгДќжаУўГівЛИіЧђМЧЯТбеЩЋКѓЗХЛиЃЌдйУўГівЛИіЧђЃЌгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГіСНДЮУўГіВЛЭЌбеЩЋЧђЕФИХТЪЃЎ
ЕФЬѕМўЯТШчЙћДгДќжаУўГівЛИіЧђМЧЯТбеЩЋКѓЗХЛиЃЌдйУўГівЛИіЧђЃЌгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓГіСНДЮУўГіВЛЭЌбеЩЋЧђЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСвдЯТВФСЯЃЌВЂАДвЊЧѓЭъГЩЯргІЕиШЮЮёЃК
РГАКЙўЕТЁЄХЗР(Leonhard Euler)ЪЧШ№ЪПЪ§бЇМвЃЌдкЪ§бЇЩЯОГЃМћЕНвдЫћЕФУћзжУќУћЕФживЊГЃЪ§ЃЌЙЋЪНКЭЖЈРэЃЌЯТУцЪЧХЗРЗЂЯжЕФвЛИіЖЈРэЃКдкЁїABCжаЃЌRКЭrЗжБ№ЮЊЭтНгдВКЭФкЧадВЕФАыОЖЃЌOКЭIЗжБ№ЮЊЦфЭтаФКЭФкаФЃЌдђ![]() .
.
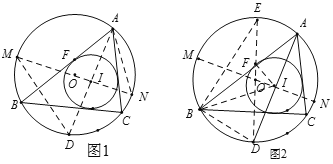
ШчЭМ1ЃЌЁбOКЭЁбIЗжБ№ЪЧЁїABCЕФЭтНгдВКЭФкЧадВЃЌЁбIгыABЯрЧаЗжгкЕуFЃЌЩшЁбOЕФАыОЖЮЊRЃЌЁбIЕФАыОЖЮЊrЃЌЭтаФOЃЈШ§НЧаЮШ§БпДЙжБЦНЗжЯпЕФНЛЕуЃЉгыФкаФIЃЈШ§НЧаЮШ§ЬѕНЧЦНЗжЯпЕФНЛЕуЃЉжЎМфЕФОрРыOIЃНdЃЌдђгаd2ЃНR2Љ2RrЃЎ
ЯТУцЪЧИУЖЈРэЕФжЄУїЙ§ГЬЃЈВПЗжЃЉЃК
бгГЄAIНЛЁбOгкЕуDЃЌЙ§ЕуIзїЁбOЕФжБОЖMNЃЌСЌНгDMЃЌAN.
ЁпЁЯD=ЁЯNЃЌЁЯDMI=ЁЯNAI(ЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШ)ЃЌ
ЁрЁїMDIЁзЁїANIЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЂйЃЌ
ЂйЃЌ
ШчЭМ2ЃЌдкЭМ1(вўШЅMDЃЌAN)ЕФЛљДЁЩЯзїЁбOЕФжБОЖDEЃЌСЌНгBEЃЌBDЃЌBIЃЌIFЃЌ
ЁпDEЪЧЁбOЕФжБОЖЃЌЁрЁЯDBE=90ЁуЃЌ
ЁпЁбIгыABЯрЧагкЕуFЃЌЁрЁЯAFI=90ЁуЃЌ
ЁрЁЯDBE=ЁЯIFAЃЌ
ЁпЁЯBAD=ЁЯE(ЭЌЛЁЫљЖддВжмНЧЯрЕШ)ЃЌ
ЁрЁїAIFЁзЁїEDBЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЂкЃЌ
ЂкЃЌ
ШЮЮёЃК(1)ЙлВьЗЂЯжЃК![]() ЃЌ
ЃЌ![]() (гУКЌRЃЌdЕФДњЪ§ЪНБэЪО)ЃЛ
(гУКЌRЃЌdЕФДњЪ§ЪНБэЪО)ЃЛ
(2)ЧыХаЖЯBDКЭIDЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
(3)ЧыЙлВьЪНзгЂйКЭЪНзгЂкЃЌВЂРћгУШЮЮё(1)ЃЌ(2)ЕФНсТлЃЌАДееЩЯУцЕФжЄУїЫМТЗЃЌЭъГЩИУЖЈРэжЄУїЕФЪЃгрВПЗжЃЛ
(4)гІгУЃКШєЁїABCЕФЭтНгдВЕФАыОЖЮЊ5cmЃЌФкЧадВЕФАыОЖЮЊ2cmЃЌдђЁїABCЕФЭтаФгыФкаФжЎМфЕФОрРыЮЊ cm.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
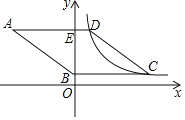
ЁОЬтФПЁПШчЭМЃЌСтаЮABCDЕФБпADЁЭyжсЃЌДЙзуЮЊЕуEЃЌЖЅЕуAдкЕкЖўЯѓЯоЃЌЖЅЕуBдкyжсЕФе§АыжсЩЯЃЌЗДБШР§КЏЪ§y=![]() ЃЈkЁй0ЃЌxЃО0ЃЉЕФЭМЯѓЭЌЪБОЙ§ЖЅЕуCЃЌDЃЎШєЕуCЕФКсзјБъЮЊ5ЃЌBE=3DEЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЃЈkЁй0ЃЌxЃО0ЃЉЕФЭМЯѓЭЌЪБОЙ§ЖЅЕуCЃЌDЃЎШєЕуCЕФКсзјБъЮЊ5ЃЌBE=3DEЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯёдкЕквЛЯѓЯогавЛИіЙЋЙВЕуЃЌЦфКсзјБъЮЊ1ЃЌдђвЛДЮКЏЪ§
ЕФЭМЯёдкЕквЛЯѓЯогавЛИіЙЋЙВЕуЃЌЦфКсзјБъЮЊ1ЃЌдђвЛДЮКЏЪ§![]() ЕФЭМЯёПЩФмЪЧЃЈ ЃЉ
ЕФЭМЯёПЩФмЪЧЃЈ ЃЉ
A. 
B. 
C. 
D. 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЪЧЪЕбщЪвжаЕФвЛжжАкЖЏзАжУЃЌ![]() дкЕиУцЩЯЃЌжЇМм
дкЕиУцЩЯЃЌжЇМм![]() ЪЧЕзБпЮЊ
ЪЧЕзБпЮЊ![]() ЕФЕШбќжБНЧШ§НЧаЮЃЌАкЖЏБлГЄ
ЕФЕШбќжБНЧШ§НЧаЮЃЌАкЖЏБлГЄ![]() ПЩШЦЕу
ПЩШЦЕу![]() а§зЊЃЌАкЖЏБл
а§зЊЃЌАкЖЏБл![]() ПЩШЦЕу
ПЩШЦЕу![]() а§зЊЃЌ
а§зЊЃЌ![]() ЃЌ
ЃЌ![]() .
.
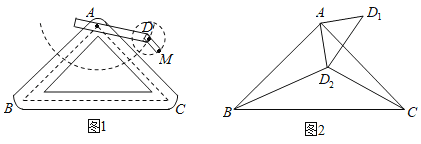
ЃЈ1ЃЉдка§зЊЙ§ГЬжаЃК
ЂйЕБ![]() Ш§ЕудкЭЌвЛжБЯпЩЯЪБЃЌЧѓ
Ш§ЕудкЭЌвЛжБЯпЩЯЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЂкЕБ![]() Ш§ЕудкЭЌвЛжБНЧШ§НЧаЮЕФЖЅЕуЪБЃЌЧѓ
Ш§ЕудкЭЌвЛжБНЧШ§НЧаЮЕФЖЅЕуЪБЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ЃЈ2ЃЉШєАкЖЏБл![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФЮЛжУгЩ
ЕФЮЛжУгЩ![]() ЭтЕФЕу
ЭтЕФЕу![]() зЊЕНЦфФкЕФЕу
зЊЕНЦфФкЕФЕу![]() ДІЃЌСЌНс
ДІЃЌСЌНс![]() ЃЌШчЭМ2ЃЌДЫЪБ
ЃЌШчЭМ2ЃЌДЫЪБ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНx+4ЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЃЈkЮЊГЃЪ§ЧвkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈЉ1ЃЌ3ЃЉЃЌBЃЈbЃЌ1ЃЉСНЕуЃЎ
ЃЈkЮЊГЃЪ§ЧвkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈЉ1ЃЌ3ЃЉЃЌBЃЈbЃЌ1ЃЉСНЕуЃЎ
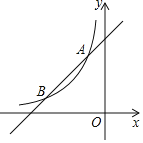
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯеввЛЕуPЃЌЪЙPA+PBЕФжЕзюаЁЃЌВЂЧѓТњзуЬѕМўЕФЕуPЕФзјБъЃЛ
ЃЈ3ЃЉСЌНгOAЃЌOBЃЌЧѓЁїOABЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЕФЫФУЖгЪЦБЭМЦЌаЮзДЭъШЋЯрЭЌЃЌЗжБ№ЪЧЮвЙњДњПЦбЇМвзцГхжЎЁЂРюЪБефЁЂеХКтЁЂЩЎвЛааЃЎАбЫФеХЭМЦЌЛьКЯдквЛЦ№ЃЎ

ЃЈ1ЃЉШєЫцЛњУўШЁвЛеХЭМЦЌЃЌдђУўЕНЁАзцГхжЎЁБЭМЦЌЕФИХТЪЪЧ__________ЃЛ
ЃЈ2ЃЉШєЫцЛњУўШЁвЛеХЭМЦЌШЛКѓЗХЛиЃЌдйЫцЛњУўШЁвЛеХЭМЦЌЃЌРћгУСаБэЛђЪїзДЭМЧѓСНДЮжСЩйгавЛДЮУўЕНЁАзцГхжЎЁБЭМЦЌЕФИХТЪЃЛ
ЃЈ3ЃЉаЁЖЋЁЂаЁЮїЁЂаЁФЯЁЂаЁББЫФЮЛЭЌбЇвРДЮУўШЁЭМЦЌЃЌШєаЁЖЋУўЕНЁАзцГхжЎЁБЭМЦЌЃЌдђЪЃЯТШ§ШЫжа(ЁЁЁЁЁЁЁЁ)
AЃЎаЁЮїУўЕНЁАРюЪБефЁБЭМЦЌЕФИХТЪДѓЁЁЁЁЁЁЁЁBЃЎаЁФЯУўЕНЁАРюЪБефЁБЭМЦЌЕФИХТЪДѓ
CЃЎаЁББУўЕНЁАРюЪБефЁБЭМЦЌЕФИХТЪДѓЁЁЁЁЁЁЁЁDЃЎШ§ШЫУўЕНЁАРюЪБефЁБЭМЦЌЕФИХТЪвЛбљДѓ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФЖЅЕуBдкxжсЩЯЃЌЕуAЁЂЕуCдкЫЋЧњЯпyЃН![]() ЃЈkЃО0ЃЌxЃО0ЃЉЩЯЃЎШєжБЯпBCЕФНтЮіЪНЮЊyЃН
ЃЈkЃО0ЃЌxЃО0ЃЉЩЯЃЎШєжБЯпBCЕФНтЮіЪНЮЊyЃН![]() xЉ2ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
xЉ2ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
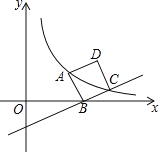
A.24B.12C.6D.4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com