
ЁОЬтФПЁПдФЖСвдЯТВФСЯЃЌВЂАДвЊЧѓЭъГЩЯргІЕиШЮЮёЃК
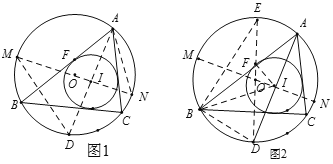
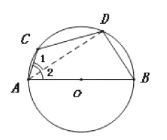
РГАКЙўЕТЁЄХЗР(Leonhard Euler)ЪЧШ№ЪПЪ§бЇМвЃЌдкЪ§бЇЩЯОГЃМћЕНвдЫћЕФУћзжУќУћЕФживЊГЃЪ§ЃЌЙЋЪНКЭЖЈРэЃЌЯТУцЪЧХЗРЗЂЯжЕФвЛИіЖЈРэЃКдкЁїABCжаЃЌRКЭrЗжБ№ЮЊЭтНгдВКЭФкЧадВЕФАыОЖЃЌOКЭIЗжБ№ЮЊЦфЭтаФКЭФкаФЃЌдђ![]() .
.
ШчЭМ1ЃЌЁбOКЭЁбIЗжБ№ЪЧЁїABCЕФЭтНгдВКЭФкЧадВЃЌЁбIгыABЯрЧаЗжгкЕуFЃЌЩшЁбOЕФАыОЖЮЊRЃЌЁбIЕФАыОЖЮЊrЃЌЭтаФOЃЈШ§НЧаЮШ§БпДЙжБЦНЗжЯпЕФНЛЕуЃЉгыФкаФIЃЈШ§НЧаЮШ§ЬѕНЧЦНЗжЯпЕФНЛЕуЃЉжЎМфЕФОрРыOIЃНdЃЌдђгаd2ЃНR2Љ2RrЃЎ
ЯТУцЪЧИУЖЈРэЕФжЄУїЙ§ГЬЃЈВПЗжЃЉЃК
бгГЄAIНЛЁбOгкЕуDЃЌЙ§ЕуIзїЁбOЕФжБОЖMNЃЌСЌНгDMЃЌAN.
ЁпЁЯD=ЁЯNЃЌЁЯDMI=ЁЯNAI(ЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШ)ЃЌ
ЁрЁїMDIЁзЁїANIЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЂйЃЌ
ЂйЃЌ
ШчЭМ2ЃЌдкЭМ1(вўШЅMDЃЌAN)ЕФЛљДЁЩЯзїЁбOЕФжБОЖDEЃЌСЌНгBEЃЌBDЃЌBIЃЌIFЃЌ
ЁпDEЪЧЁбOЕФжБОЖЃЌЁрЁЯDBE=90ЁуЃЌ
ЁпЁбIгыABЯрЧагкЕуFЃЌЁрЁЯAFI=90ЁуЃЌ
ЁрЁЯDBE=ЁЯIFAЃЌ
ЁпЁЯBAD=ЁЯE(ЭЌЛЁЫљЖддВжмНЧЯрЕШ)ЃЌ
ЁрЁїAIFЁзЁїEDBЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЂкЃЌ
ЂкЃЌ
ШЮЮёЃК(1)ЙлВьЗЂЯжЃК![]() ЃЌ
ЃЌ![]() (гУКЌRЃЌdЕФДњЪ§ЪНБэЪО)ЃЛ
(гУКЌRЃЌdЕФДњЪ§ЪНБэЪО)ЃЛ
(2)ЧыХаЖЯBDКЭIDЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
(3)ЧыЙлВьЪНзгЂйКЭЪНзгЂкЃЌВЂРћгУШЮЮё(1)ЃЌ(2)ЕФНсТлЃЌАДееЩЯУцЕФжЄУїЫМТЗЃЌЭъГЩИУЖЈРэжЄУїЕФЪЃгрВПЗжЃЛ
(4)гІгУЃКШєЁїABCЕФЭтНгдВЕФАыОЖЮЊ5cmЃЌФкЧадВЕФАыОЖЮЊ2cmЃЌдђЁїABCЕФЭтаФгыФкаФжЎМфЕФОрРыЮЊ cm.

ЁОД№АИЁП(1)R-dЃЛ(2)BD=IDЃЌРэгЩМћНтЮіЃЛ(3)МћНтЮіЃЛ(4)![]() .
.
ЁОНтЮіЁП
(1)жБНгЙлВьПЩЕУЃЛ
(2)гЩШ§НЧаЮФкаФЕФаджЪПЩЕУЁЯBAD=ЁЯCADЃЌЁЯCBI=ЁЯABIЃЌгЩдВжмНЧЖЈРэПЩЕУЁЯDBC=ЁЯCADЃЌдйИљОнШ§НЧаЮЭтНЧЕФаджЪМДПЩЧѓЕУЁЯBID=ЁЯDBIЃЌМЬЖјПЩжЄЕУBD=IDЃЛ
(3)гІгУ(1)(2)НсТлМДПЩЃЛ
(4)жБНгДњШыНсТлНјааМЦЫуМДПЩЃЎ
(1)ЁпOЁЂIЁЂNШ§ЕуЙВЯпЃЌ
ЁрOI+INЃНONЃЌ
ЁрINЃНONЉOIЃНRЉdЃЌ
ЙЪД№АИЮЊЃКRЉdЃЛ
(2)BD=IDЃЌРэгЩШчЯТЃК
ЁпЕуIЪЧЁїABCЕФФкаФЃЌ
ЁрЁЯBAD=ЁЯCADЃЌЁЯCBI=ЁЯABIЃЌ
ЁпЁЯDBC=ЁЯCADЃЌЁЯBID=ЁЯBAD+ЁЯABIЃЌЁЯDBI=ЁЯDBC+ЁЯCBIЃЌ
ЁрЁЯBID=ЁЯDBIЃЌ
ЁрBD=IDЃЛ
(3)гЩ(2)жЊЃКBD=IDЃЌ
гж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрDEЁЄIF=IMЁЄINЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]() ЃЛ
ЃЛ
(4)гЩ(3)жЊЃК![]() ЃЌ
ЃЌ
АбR=5ЃЌr=2ДњШыЕУЃК![]() ЃЌ
ЃЌ
Ёпd>0ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧаББп
ЪЧаББп![]() ЕФжаЕуЃЎЕу
ЕФжаЕуЃЎЕу![]() ДгЕу
ДгЕу![]() ГіЗЂвд
ГіЗЂвд![]() ЕФЫйЖШЯђЕу
ЕФЫйЖШЯђЕу![]() дЫЖЏЃЌЕу
дЫЖЏЃЌЕу![]() ЭЌЪБДгЕу
ЭЌЪБДгЕу![]() ГіЗЂвдвЛЖЈЕФЫйЖШбиЩфЯп
ГіЗЂвдвЛЖЈЕФЫйЖШбиЩфЯп![]() ЗНЯђдЫЖЏЃЌЙцЖЈЕБЕу
ЗНЯђдЫЖЏЃЌЙцЖЈЕБЕу![]() ЕНжеЕу
ЕНжеЕу![]() ЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЕФЪБМфЮЊ
ЪБЭЃжЙдЫЖЏЃЎЩшдЫЖЏЕФЪБМфЮЊ![]() УыЃЌСЌНг
УыЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЬюПеЃК![]() ______
______![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЧвЕу
ЧвЕу![]() дЫЖЏЕФЫйЖШвВЪЧ
дЫЖЏЕФЫйЖШвВЪЧ![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШєЖЏЕу![]() вд
вд![]() ЕФЫйЖШбиЩфЯп
ЕФЫйЖШбиЩфЯп![]() ЗНЯђдЫЖЏЃЌдкЕу
ЗНЯђдЫЖЏЃЌдкЕу![]() ЁЂЕу
ЁЂЕу![]() дЫЖЏЙ§ГЬжаЃЌШчЙћДцдкФГИіЪБМф
дЫЖЏЙ§ГЬжаЃЌШчЙћДцдкФГИіЪБМф![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЕФУцЛ§ЪЧ
ЕФУцЛ§ЪЧ![]() УцЛ§ЕФСНБЖЃЌЧыФуЧѓГіЪБМф
УцЛ§ЕФСНБЖЃЌЧыФуЧѓГіЪБМф![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
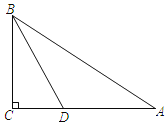
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌBDЦНЗжЁЯABCЃЎЧѓзїЁбOЃЌЪЙЕУЕуOдкБпABЩЯЃЌЧвЁбOОЙ§BЁЂDСНЕуЃЛВЂжЄУїACгыЁбOЯрЧаЃЎЃЈГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() ЭјТчБШ
ЭјТчБШ![]() ЭјТчЕФДЋЪфЫйЖШПь10БЖвдЩЯЃЌвђДЫШЫУЧЖд
ЭјТчЕФДЋЪфЫйЖШПь10БЖвдЩЯЃЌвђДЫШЫУЧЖд![]() ВњЦЗГфТњЦкД§.ЛЊЮЊМЏЭХМЦЛЎ2020ФъдЊдТПЊЪМЯњЪлвЛПю
ВњЦЗГфТњЦкД§.ЛЊЮЊМЏЭХМЦЛЎ2020ФъдЊдТПЊЪМЯњЪлвЛПю![]() ВњЦЗ.ИљОнЪаГЁгЊЯњВПЕФЙцЛЎЃЌИУВњЦЗЕФЯњЪлМлИёНЋЫцЯњЪлдТЗнЕФБфЛЏЖјБфЛЏ.ШєИУВњЦЗЕк
ВњЦЗ.ИљОнЪаГЁгЊЯњВПЕФЙцЛЎЃЌИУВњЦЗЕФЯњЪлМлИёНЋЫцЯњЪлдТЗнЕФБфЛЏЖјБфЛЏ.ШєИУВњЦЗЕк![]() ИідТЃЈ
ИідТЃЈ![]() ЮЊе§ећЪ§ЃЉЯњЪлМлИёЮЊ
ЮЊе§ећЪ§ЃЉЯњЪлМлИёЮЊ![]() дЊ/ЬЈЃЌ
дЊ/ЬЈЃЌ![]() гы
гы![]() ТњзуШчЭМЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕЃКЧвЕк
ТњзуШчЭМЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕЃКЧвЕк![]() ИідТЕФЯњЪлЪ§СП
ИідТЕФЯњЪлЪ§СП![]() ЃЈЭђЬЈЃЉгы
ЃЈЭђЬЈЃЉгы![]() ЕФЙиЯЕЮЊ
ЕФЙиЯЕЮЊ![]() .
.
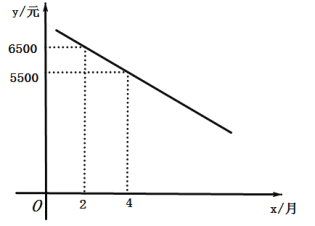
ЃЈ1ЃЉИУВњЦЗЕк6ИідТУПЬЈЯњЪлМлИёЮЊ______дЊЃЛ
ЃЈ2ЃЉЧѓИУВњЦЗЕкМИИідТЕФЯњЪлЖюзюДѓЃПИУдТЕФЯњЪлМлИёЪЧЖрЩйдЊ/ЬЈЃП
ЃЈ3ЃЉШєЛЊЮЊЖЪТЛсвЊЧѓЯњЪлИУВњЦЗЕФдТЯњЪлЖюВЛЕЭгк27500ЭђдЊЃЌдђдЄМЦЯњЪлВПЗћКЯЯњЪлвЊЧѓЕФЪЧФФМИИідТЃП
ЃЈ4ЃЉШєУПЯњЪл1ЭђЬЈИУВњЦЗашвЊдкЯњЪлЖюжаПлГ§![]() дЊЭЦЙуЗбгУЃЌЕБ
дЊЭЦЙуЗбгУЃЌЕБ![]() ЪБЯњЪлРћШѓзюДѓжЕЮЊ22500ЭђдЊЪБЃЌЧѓ
ЪБЯњЪлРћШѓзюДѓжЕЮЊ22500ЭђдЊЪБЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ABЪЧЁб0ЕФжБОЖ,ЕуCдкЁб0ЩЯ,DЪЧ![]() жаЕу,ШєЁЯBAC=70Ёу,ЧѓЁЯC.
жаЕу,ШєЁЯBAC=70Ёу,ЧѓЁЯC.
ЯТУцЪЧаЁіЉЕФНтЗЈ,ЧыАяЫћВЙГфЭъећ:
Нт:дкЁб0жа,
ЁпDЪЧ![]() ЕФжаЕу
ЕФжаЕу
ЁрBD=CD.
ЁрЁЯ1=ЁЯ2( )(ЬюЭЦРэЕФвРОн).
ЁпЁЯBAC=70Ёу,
ЁрЁЯ2=35Ёу.
ЁпABЪЧЁб0ЕФжБОЖ,
ЁрЁЯADB=90Ёу( )(ЬюЭЦРэЕФвРОн).
ЁрЁЯB=90Ёу-ЁЯ2=55Ёу.
ЁпAЁЂBЁЂCЁЂDЫФИіЕуЖМдкЁб0ЩЯ,
ЁрЁЯC+ЁЯB=180Ёу( )(ЬюЭЦРэЕФвРОн).
ЁрЁЯC=180Ёу-ЁЯB= (ЬюМЦЫуНсЙћ).
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕx0yжа,ЖдгкЭМаЮG,ШєДцдквЛИіе§ЗНаЮІУ,етИіе§ЗНаЮЕФФГЬѕБпгыxжсДЙжБ,ЧвЭМаЮGЩЯЕФЫљгаЕФЕуЖМдкИУе§ЗНаЮЕФФкВПЛђепБпЩЯ,дђГЦИУе§ЗНаЮІУЮЊЭМаЮGЕФвЛИіе§ИВИЧ.КмЯдШЛ,ШчЙћЭМаЮGДцдквЛИіе§ИВИЧ,дђЫќЕФе§ИВИЧгаЮоЪ§Иі,ЮвУЧНЋЭМаЮGЕФЫљгае§ИВИЧжаБпГЄзюаЁЕФвЛИі,ГЦЮЊЫќЕФНєИВИЧ.ШчЭМЫљЪО,ЭМаЮGЮЊШ§ЬѕЯпЖЮКЭвЛИідВЛЁзщГЩЕФЗтБеЭМаЮ,ЭМжаЕФШ§Иіе§ЗНаЮОљЮЊЭМаЮGЕФе§ИВИЧ,Цфжае§ЗНаЮABCDОЭЪЧЭМаЮGЕФНєИВИЧ.

(1)ЖдгкАыОЖЮЊ2ЕФЁб0,ЫќЕФНєИВИЧЕФБпГЄЮЊ .
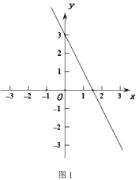
(2)ШчЭМ1,ЕуPЮЊжБЯпy=-2x+3ЩЯвЛЖЏЕу,ШєЯпЖЮOPЕФНєИВИЧЕФБпГЄЮЊ2,ЧѓЕуPЕФзјБъ;
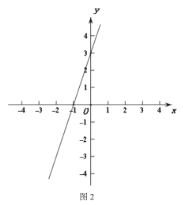
(3)ШчЭМ2,жБЯпy=3x+3гыxжс,yжсЗжБ№НЛгкA,B,
Ђйвд0ЮЊдВаФ,rЮЊАыОЖЕФЁб0гыЯпЖЮABгаЙЋЙВЕу,ЧвгЩЁб0гыЯпЖЮABзщГЩЕФЭМаЮGЕФНєИВИЧЕФБпГЄаЁгк4,жБНгаДГіrЕФШЁжЕЗЖЮЇ;
ЂкШєдкХзЮяЯпy=ax2+2ax-2(aЁй0)ЩЯДцдкЕуC,ЪЙЕУЁїABCЕФНєИВИЧЕФБпГЄЮЊ3,жБНгаДГіaЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() ЕФБпГЄЪЧ
ЕФБпГЄЪЧ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ЭЌЪБДгЕу
ЭЌЪБДгЕу![]() ГіЗЂЃЌвд
ГіЗЂЃЌвд![]() ЕФЫйЖШЗжБ№би
ЕФЫйЖШЗжБ№би![]() дЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ
дЫЖЏЃЌЩшдЫЖЏЪБМфЮЊ![]() ЃЌЫФБпаЮ
ЃЌЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЭМЯѓДѓжТЮЊЃЈ ЃЉ
ЕФКЏЪ§ЙиЯЕЭМЯѓДѓжТЮЊЃЈ ЃЉ
A.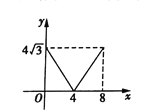 B.
B.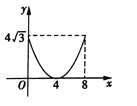
C.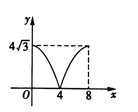 D.
D.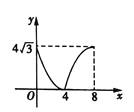
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
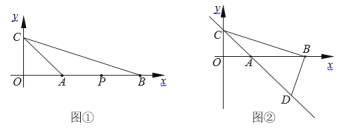
ЁОЬтФПЁПЖЈвхЃКЕуPдкЁїABCЕФБпЩЯЃЌЧвгыЁїABCЕФЖЅЕуВЛжиКЯЃЎШєТњзуЁїPABЁЂЁїPBCЁЂЁїPACжСЩйгавЛИіШ§НЧаЮгыЁїABCЯрЫЦЃЈЕЋВЛШЋЕШЃЉЃЌдђГЦЕуPЮЊЁїABCЕФздЯрЫЦЕуЃЎШчЭМЂйЃЌвбжЊЕуAЁЂBЁЂCЕФзјБъЗжБ№ЮЊЃЈ1ЃЌ0ЃЉЁЂЃЈ3ЃЌ0ЃЉЁЂЃЈ0ЃЌ1ЃЉЃЎ
ЃЈ1ЃЉШєЕуPЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌЧѓжЄЕуPЪЧЁїABCЕФздЯрЫЦЕуЃЛ
ЃЈ2ЃЉЧѓГ§ЕуЃЈ2ЃЌ0ЃЉЭтЁїABCЫљгаздЯрЫЦЕуЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌЙ§ЕуBзїDBЁЭBCНЛжБЯпACгкЕуDЃЌдкжБЯпACЩЯЪЧЗёДцдкЕуGЃЌЪЙЁїGBDгыЁїGBCгаЙЋЙВЕФздЯрЫЦЕуЃПШєДцдкЃЌЧыОйР§ЫЕУїЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com