
【题目】在一个不透明的袋子中,装有除颜色外都完全相同的4个红球和若干个黄球.
![]() 如果从袋中任意摸出一个球是红球的概率为
如果从袋中任意摸出一个球是红球的概率为![]() ,那么袋中有黄球多少个?
,那么袋中有黄球多少个?
![]() 在
在![]() 的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
【答案】(1)袋中有黄球有2个(2)![]()
【解析】
![]() 设袋中黄球有x个,根据任意摸出一个球是红球的概率为
设袋中黄球有x个,根据任意摸出一个球是红球的概率为![]() 列出关于x的方程,解之可得;
列出关于x的方程,解之可得;![]() 列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.
列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.
![]() 设袋中黄球有x个,
设袋中黄球有x个,
根据题意,得:![]() ,
,
解得![]() ,
,
经检验![]() 是原分式方程的解,
是原分式方程的解,
![]() ,即袋中有黄球有2个;
,即袋中有黄球有2个;
![]() 列表如下:
列表如下:
红 | 红 | 红 | 红 | 黄 | 黄 | |
红 |
|
|
|
|
|
|
红 |
|
|
|
|
|
|
红 |
|
|
|
|
|
|
红 |
|
|
|
|
|
|
黄 |
|
|
|
|
|
|
黄 |
|
|
|
|
|
|
由表知共有36种等可能结果,其中两次摸出不同颜色球的有16种结果,
所以两次摸出不同颜色球的概率为![]() .
.


科目:初中数学 来源: 题型:
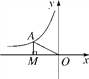
【题目】如图,反比例函数y=![]() 的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于点M,O是原点.若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于点M,O是原点.若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学实践活动小组要测量学校附近楼房CD的高度,在水平底面A处安置侧倾器测得楼房CD顶部点D的仰角为30°,向前走20米到达E处,测得点D的仰角为60°.已知侧倾器AB的高度为1.6米,则楼房CD的高度约为(结果精确到0.1米)( )
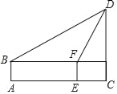
A. 30米 B. 18.9米 C. 32.6米 D. 30.6米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,22,3分)如图1,△ABC中,∠C=90°,∠ABC=30°,AC=m,延长CB至点D,使BD=AB.
①求∠D的度数;
②求tan75°的值.
(2)如图2,点M的坐标为(2,0),直线MN与y轴的正半轴交于点N,∠OMN=75°.求直线MN的函数表达式.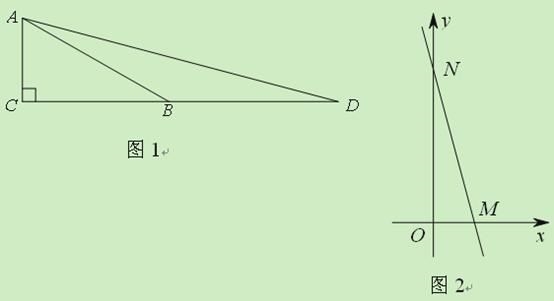
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的右端点运动到M点的时刻为0,用t(秒)表示l的运动时间.

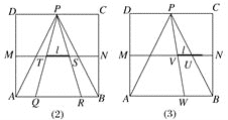
(1)请你针对图(1)(2)(3)中l位于不同位置的情形分别画出在△PAB内相应的盲区,并在盲区内涂上阴影.
(2)设△PAB内的盲区面积是y(平方单位),在下列条件下,求出用t表示y的函数关系式.
①1≤t≤2;
②2≤t≤3;
③3≤t≤4.
根据①~③中得到的结论,请你简单概括y随t变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AO是![]() 的半径,AC为
的半径,AC为![]() 的弦,点F为
的弦,点F为![]() 的中点,OF交AC于点E,AC=8,EF=2.
的中点,OF交AC于点E,AC=8,EF=2.
(1)求AO的长;
(2)过点C作CD⊥AO,交AO延长线于点D,求sin∠ACD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正三角形和正方形内接于同一个圆;如图②,正方形和正五边形内接于同一个圆;如图③,正五边形和正六边形内接于同一个圆;…;则对于图①来说,BD可以看作是正_____边形的边长;若正n边形和正(n+1)边形内接于同一个圆,连接与公共顶点相邻同侧两个不同正多边形的顶点可以看做是_____边形的边长.
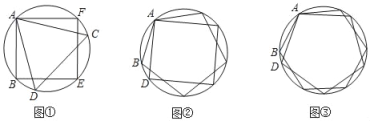
查看答案和解析>>
科目:初中数学 来源: 题型:
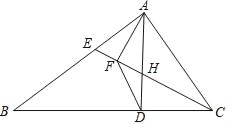
【题目】如图,在△ABC中,点D在边BC上,∠CAD=∠B,点E在边AB上,联结CE交AD于点H,点F在CE上,且满足CFCE=CDBC.
(1)求证:△ACF∽△ECA;
(2)当CE平分∠ACB时,求证:![]() =
=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com