
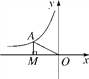
【题目】如图,反比例函数y=![]() 的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于点M,O是原点.若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
的图象在第二象限内,点A是图象上的任意一点,AM⊥x轴于点M,O是原点.若S△AOM=3,求该反比例函数的解析式,并写出自变量的取值范围.
【答案】y=-![]() (x<0)
(x<0)
【解析】
试题
要求反比例函数的解析式就是要求比例系数k的值. 观察图形可以发现,△AOM恰好是与比例系数k的几何意义密切相关的一个典型图形,易知S△AOM=![]() . 据此,结合已知条件不难求得k的绝对值,再根据反比例函数图象所在的象限,容易判定k的符号,进而获得k的值. 根据题目中给出的图象可知,该函数的图象只在第二象限内,故自变量x的取值范围也就确定了.
. 据此,结合已知条件不难求得k的绝对值,再根据反比例函数图象所在的象限,容易判定k的符号,进而获得k的值. 根据题目中给出的图象可知,该函数的图象只在第二象限内,故自变量x的取值范围也就确定了.
试题解析:
根据题目中△AOM的特征以及反比例函数中比例系数k的几何意义可知,S△AOM=![]() .
.
∵S△AOM=3,
∴![]() ,
,
∴![]() .
.
由图可知,该反比例函数的图象在第二象限内,根据反比例函数的图象与性质可知k<0,故k=-6,即该反比例函数解析式为![]() .
.
由于图中函数的图象只有第二象限内的一支,所以自变量x的取值范围为x<0.
因此,该函数的解析式及自变量取值范围应为:![]() (x<0).
(x<0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
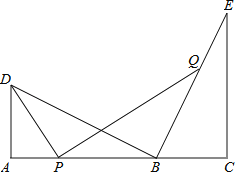
【题目】如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;
(i)当点P与A,B两点不重合时,求![]() 的值;
的值;
(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
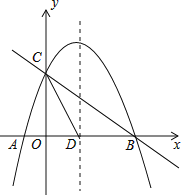
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的表达式;
求抛物线的表达式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
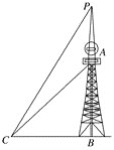
【题目】哈尔滨龙塔坐落于经济技术开发区,在钢结构塔中位居亚洲第一,世界第二.在塔上有一个室外观光平台A可以欣赏的哈尔滨市的全景,室外观光平台中央位置A距离塔顶P约146米,一名同学站在C处观察A点的仰角为45°,观察P点的仰角为60.5°,则龙塔PB的高度为______________.(已知:tan 60.5°=1.77)(精确到1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
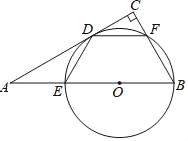
【题目】如图,点O是Rt△ABC的AB边上一点,∠ACB=90°,⊙O与AC相切于点D,与边AB,BC分别相交于点E,F.
(1)求证:DE=DF;
(2)当BC=3,sinA=![]() 时,求AE的长.
时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外都完全相同的4个红球和若干个黄球.
![]() 如果从袋中任意摸出一个球是红球的概率为
如果从袋中任意摸出一个球是红球的概率为![]() ,那么袋中有黄球多少个?
,那么袋中有黄球多少个?
![]() 在
在![]() 的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com