
【题目】如图1,矩形ABCD中,AD=2,AB=3,点E,F分别在边AB,BC上,且BF=FC,连接DE,EF,并以DE,EF为边作DEFG.
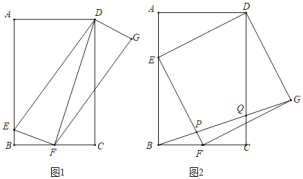
(1)连接DF,求DF的长度;
(2)求DEFG周长的最小值;
(3)当DEFG为正方形时(如图2),连接BG,分别交EF,CD于点P、Q,求BP:QG的值.
【答案】(1)![]() ;(2)6
;(2)6![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)平行四边形DEFG对角线DF的长就是Rt△DCF的斜边的长,由勾股定理求解;
(2)平行四边形DEFG周长的最小值就是求邻边2(DE+EF)最小值,DE+EF的最小值就是以AB为对称轴,作点F的对称点M,连接DM交AB于点N,点E与N点重合时即DE+EF=DM时有最小值,在Rt△DMC中由勾股定理求DM的长;
(3)平行四边形DEFG为矩形时有两种情况,一是一般矩形,二是正方形,分类用全等三角形判定与性质,等腰直角三角形判定与性质,三角形相似的判定与性质和勾股定理求解.
解:(1)如图1所示:
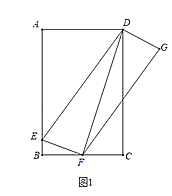
∵四边形ABCD是矩形,
∠C=90°,AD=BC,AB=DC,
∵BF=FC,AD=2;
∴FC=1,
∵AB=3;
∴DC=3,
在Rt△DCF中,由勾股定理得,
∴DF=![]() =
=![]() =
=![]() ;
;
(2)如图2所示:
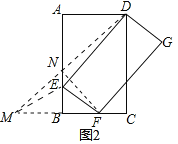
作点F关直线AB的对称点M,连接DM交AB于点N,
连接NF,ME,点E在AB上是一个动点,
①当点E不与点N重合时点M、E、D可构成一个三角形,
∴ME+DE>MD,
②当点E与点N重合时点M、E(N)、D在同一条直线上,
∴ME+DE=MD
由①和②DE+EF的值最小时就是点E与点N重合时,
∵MB=BF,
∴MB=1,
∴MC=3,
又∵DC=3,
∴△MCD是等腰直角三角形,
∴MD=![]() =
=![]() =3
=3![]() ,
,
∴NF+DN=MD=3![]() ,
,
∴l平行四边形DEFG=2(NF+DF)=6![]() ;
;
(3)设AE=x,则BE=3﹣x,
∵平行四边形DEFG为矩形,∴∠DEF=90°,
∵∠AED+∠BEF=90°,∠BEF+∠BFE=90°,
∴∠AED=∠BFE,
又∵∠A=∠EBF=90°,
∴△DAE∽△EBF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:x=1,或x=2
①当AE=1,BE=2时,过点B作BH⊥EF,
如图3(甲)所示:
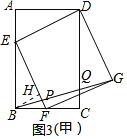
∵平行四边形DEFG为矩形,
∴∠A=∠ABF=90°,
又∵BF=1,AD=2,
∴在△ADE和△BEF中,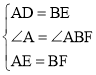 ,
,
∴△ADE≌△BEF中(SAS),
∴DE=EF,
∴矩形DEFG是正方形;
在Rt△EBF中,由勾股定理得:
EF=![]() =
=![]() =
=![]() ,
,
∴BH=![]() =
=![]() ,
,
又∵△BEF~△HBF,
∴![]() =
=![]() ,
,
HF=![]() =
=![]() =
=![]() ,
,
在△BPH和△GPF中有:∠BPH=∠GPF,∠BHP=∠GFP,
∴△BPH∽△GPF,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴PF=![]() HF=
HF=![]() ,
,
又∵EP+PF=EF,
∴EP=![]() ﹣
﹣![]() =
=![]() ,
,
又∵AB∥BC,EF∥DG,
∴∠EBP=∠DQG,∠EPB=∠DGQ,
∴△EBP∽△DQG(AA),
∴![]() =
=![]() =
=![]() =
=![]() ,
,
②当AE=2,BE=1时,过点G作GH⊥DC,
如图3(乙)所示:

∵DEFG为矩形,
∴∠A=∠EBF=90°,
∵AD=AE=2,BE=BF=1,
∴在Rt△ADE和Rt△EFB中,由勾股定理得:
∴ED=![]() =2
=2![]() ,
,
EF=![]() =
=![]() =
=![]() ,
,
∴∠ADE=45°,
又∵四边形DEFG是矩形,
∴EF=DG,∠EDG=90°,
∴DG=![]() ,∠HDG=45°,
,∠HDG=45°,
∴△DHG是等腰直角三角形,
∴DH=HG=1,
在△HGQ和△BCQ中有,∠GHQ=∠BCQ,∠HQG=∠CQB,
∴△HGQ∽△BCQ,
∴![]() =
=![]() =
=![]() ,
,
∵HC=HQ+CQ=2,
∴HQ=![]() ,
,
又∵DQ=DH+HQ,
∴DQ=1+![]() =
=![]() ,
,
∵AB∥DC,EF∥DG,
∴∠EBP=∠DQG,∠EPB=∠DGQ,
∴△EBP∽△DQG(AA),
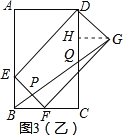
∴![]() =
=![]() ,
,
综合所述,BP:QG的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,已知
,已知![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)如图2,若点![]() 是直线
是直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴的平行线交直线
轴的平行线交直线![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,求
时,求![]() 的面积;
的面积;
(3)若点![]() 为抛物线上的一个动点,以点
为抛物线上的一个动点,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,当
,当![]() 在运动过程中与直线
在运动过程中与直线![]() 相切时,求点
相切时,求点![]() 的坐标(请直接写出答案).
的坐标(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=![]() ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是_______.
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线,垂足为A.作y轴的垂线,垂足为C.点D从O出发,沿y轴正方向以每秒1个单位长度运动;点E从O出发,沿x轴正方向以每秒3个单位长度运动;点F从B出发,沿BA方向以每秒2个单位长度运动.当点E运动到点A时,三点随之停止运动,运动过程中△ODE关于直线DE的对称图形是△O′DE,设运动时间为t.
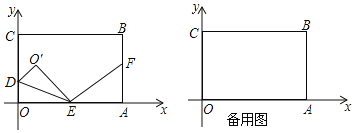
(1)用含t的代数式分别表示点E和点F的坐标;
(2)若△ODE与以点A,E,F为顶点的三角形相似,求t的值;
(3)当t=2时,求O′点在坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外都完全相同的4个红球和若干个黄球.
![]() 如果从袋中任意摸出一个球是红球的概率为
如果从袋中任意摸出一个球是红球的概率为![]() ,那么袋中有黄球多少个?
,那么袋中有黄球多少个?
![]() 在
在![]() 的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
的条件下如果从袋中摸出一个球记下颜色后放回,再摸出一个球,用列表或画树状图的方法求出两次摸出不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).
(1)小红摸出标有数3的小球的概率是多少?.
(2)请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.
(3)求点P(x,y)在函数y=﹣x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过A(0,﹣4)和B(2,0)两点.
(1)求c的值及a,b满足的关系式;
(2)若抛物线在A和B两点间,从左到右上升,求a的取值范围;
(3)抛物线同时经过两个不同的点M(p,m),N(﹣2﹣p,n).
①若m=n,求a的值;
②若m=﹣2p﹣3,n=2p+1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,![]() 在地面上,支架
在地面上,支架![]() 是底边为
是底边为![]() 的等腰直角三角形,摆动臂长
的等腰直角三角形,摆动臂长![]() 可绕点
可绕点![]() 旋转,摆动臂
旋转,摆动臂![]() 可绕点
可绕点![]() 旋转,
旋转,![]() ,
,![]() .
.
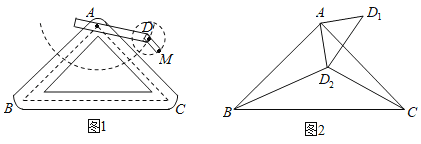
(1)在旋转过程中:
①当![]() 三点在同一直线上时,求
三点在同一直线上时,求![]() 的长;
的长;
②当![]() 三点在同一直角三角形的顶点时,求
三点在同一直角三角形的顶点时,求![]() 的长.
的长.
(2)若摆动臂![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 的位置由
的位置由![]() 外的点
外的点![]() 转到其内的点
转到其内的点![]() 处,连结
处,连结![]() ,如图2,此时
,如图2,此时![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com