练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，ΔABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF的度数是（     ）

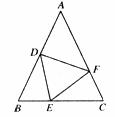
    A．75°     B．70°     C．65°     D．60°


    C

    【解析】因为AB=AC，∠A=50°，所以∠B=∠C=65°，又因为BD=CE，BE=CF，所以ΔBDE≌ΔCEF,所以∠BED=∠CFE，因为∠CFE+∠CEF=180°-65°=115°，所以∠BED+∠CEF=115°，所以∠DEF=180°-（∠BED+∠CEF）=180°-115°=65°，

    故选C.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，抛物线y=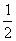x2+bx－2与x轴交于A、B两点，与y轴交于C点，且A（一1，0）．

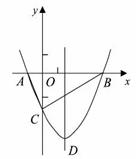
    （1）求抛物线的解析式及顶点D的坐标；

    （2）判断△ABC的形状，证明你的结论；

    （3）点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列运算正确的是（  ）．

    A．x2•x3=x6     B．x6÷x5=x    C．（﹣x2）4=x6    D．x2+x3=x5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    D．

    【解析】根据题意得：∠BAE=∠ADC=∠AFE=90°，∴∠AEF+∠EAF=90°，∠DAC+∠ACD=90°，∴∠AEF=∠ACD，∴①中两三角形相似； 容易判断△AFE∽△BAE，得，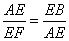

    又∵AE=ED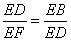，∴而∠BED=∠BED，∴△FED∽△DEB．故②正确；

    ∵AB∥CD，∴∠BAC=∠GCD，∵∠ABE=∠DAF，∠EBD=∠EDF，且∠ABG=∠ABE+∠EBD，

    ∴∠ABG=∠DAF+∠EDF=∠DFC；∵∠ABG=∠DFC，∠BAG=∠DCF，∴△CFD∽△ABG，故③正确；所以相似的有①②③．

    故选D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0．5h（休息前后的速度一致），如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．则当乙车行驶       小时后，两车恰好相距50km．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图①是一块瓷砖的图案，用这种瓷砖铺设地面，如果铺设成如图②的图案，其中完整的圆一共有5个，如果铺设成如图③的图案，其中完整的圆一共有13个，如果铺设成如图④的图案，其中完整的圆一共有25个，以此规律下去，第10个图中，完整的圆一共有（    ）．

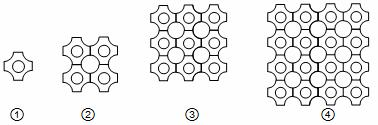
    A．100个         B．101个       C．181个        D．221个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，D，E分别是AB，AC上的点（DEBC），当        或        或     时，△ADE与△ABC相似。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果将抛物线向下平移1个单位，那么所得新抛物线的表达式是（     ）

    A．       B．

    C．            D．．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    中国象棋红方棋子按兵种不同分布如下：1个帅，5个兵，“士、象、马、车、炮”各两个，将所有棋子反面朝上放在棋盘中，任取一个不是士、象、帅的概率是__________．

    查看答案和解析>>

    同步练习册答案