
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则当乙车行驶 小时后,两车恰好相距50km.

(1)y=x2+4x+3;
(2)见解析;
(3)①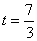 ②能,点P的坐标
②能,点P的坐标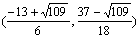 或
或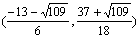
【解析】(1)∵二次函数的图象过点A(-3,0)、B(-1,0),∴设该函数的函数关系式为y=a(x+3)(x+1) ,
又∵函数的图象过点C(0,3),∴3a=3, a=1 ,
∴二次函数的函数关系式为y=(x+3)(x+1),即y=x2+4x+3 ;
(2)∵点P的坐标为(-4,m),∴(-4)2+4×(-4)+3=m,得m=3,则点P的坐标为(-4,3),又点C的坐标为(0,3),∴PC∥OQ , PC=4 ,∵Q是一次函数y=kx-4k的图象与x轴的交点,∴当y=0时,kx-4k=0,即k(x-4)=0
∵k≠0,∴x=4,∴点Q的坐标为(4,0) ,∵PC=OQ=4,∴四边形POQC是平行四边形,∴∠OPC=∠AQC ;
(3)①连结AN,则有AM=3t,CN=t∵点C的坐标为C(0,3), ∴OC=3,由(2)得OQ=4, ∴CQ=5,∴QN=5-t ,过点N作NG⊥AQ于点G,
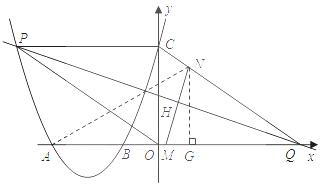
则△QGN∽△QOC,∴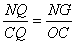 ,
,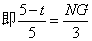 ,∴NG=
,∴NG=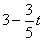 ,∴△AMN的面积为S与时间t的函数关系式为
,∴△AMN的面积为S与时间t的函数关系式为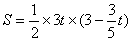 即
即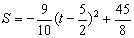 ,
,
∵点M从点A运动到点Q需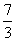 秒,点N从点C运动到点Q需5秒,∴点M先到达点Q,即
秒,点N从点C运动到点Q需5秒,∴点M先到达点Q,即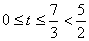 ,∵当
,∵当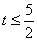 时,S随着t的增大而增大,∴当△AMN的面积最大时,
时,S随着t的增大而增大,∴当△AMN的面积最大时, 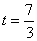 ,
,
②直线PQ能垂直平分线段MN ,
当NQ=MQ,且PQ与MN的交点H是MN的中点时,PQ垂直平分线段MN,
∵QN=5 -t,MQ=7-3t,则5-t=7-3t, ∴t=1
-t,MQ=7-3t,则5-t=7-3t, ∴t=1
即t =1,且PQ与MN的交点H是MN的中点时,直线PQ垂直平分线段MN,
=1,且PQ与MN的交点H是MN的中点时,直线PQ垂直平分线段MN,
此时NQ=MQ=4,点M的坐标为(0,0)
由①可得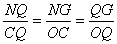 ,
,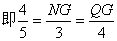 ,
,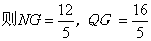 ,
,
∴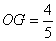 , ∴点N的坐标为(
, ∴点N的坐标为(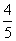 ,
,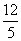 ),∴线段MN的中点H的坐标为(
),∴线段MN的中点H的坐标为(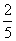 ,
,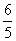 )
)
∴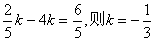 ,
,
∴线段MN的垂直平分线段PQ的函数关系式为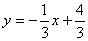
∵点P是直线PQ与抛物线y=x2+4x+3的公 共点,∴
共点,∴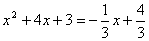
解得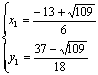 ,
,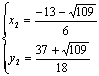 ,
,
∴点P的坐标为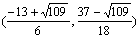 或
或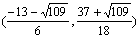


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A( ,3),B(
,3),B(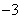 ,1),C(
,1),C(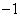 ,3).
,3).
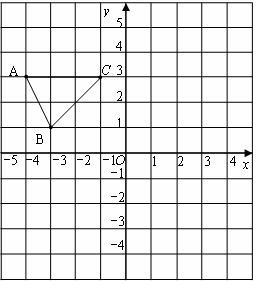
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△AB C关于原点O成中心对称,画出△A2B2C2.
C关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
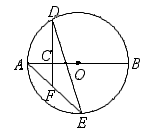
如图,AB是⊙O的直径且AB=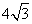 ,点C是OA的中点,过点C[,作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE·AF的值为( ).
,点C是OA的中点,过点C[,作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE·AF的值为( ).
A .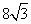 B.
B. C.
C. D.
D.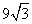
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形AOCD的顶点A的坐标是(0,4).动点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,同时动点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.当其中一点到达终点时,另一点也停止运动.设运动时间为t(秒),当t=2(秒)时,PQ= .解答下列问题:
.解答下列问题:

(1)求点D的坐标;
(2)直接写出t的取值范围;
(3)连接AQ并延长交x轴于点E,把AQ沿AD翻折,点Q落在CD延长线上点F处,连接EF.
①t为何值时,PQ∥AF;
②△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
铜陵学院毕业生小张响应国家“自主创业”的号召,投资开办了一个装饰品商店,该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系: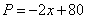 (1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:
(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系: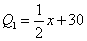 (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)第25天该商店的日销售利润为多少元?
(2)试写出该商店日销售利润y(元)关于销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com