
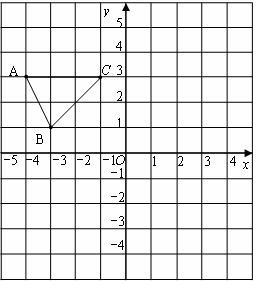
如图,抛物线y=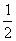 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
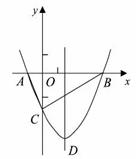
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
1)y= x2-
x2-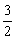 x-2;(
x-2;(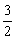 , -
, -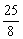 );(2)△ABC是直角三角形;(3)
);(2)△ABC是直角三角形;(3)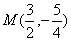 ,△ACM最小周长是
,△ACM最小周长是 .
.
【解析】(1)∵点A(-1,0)在抛物线y= x2 + bx-2上,∴
x2 + bx-2上,∴ × (-1 )2 + b
× (-1 )2 + b × (-1) –2 = 0,解得
× (-1) –2 = 0,解得
b =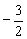 ,∴抛物线的解析式为y=
,∴抛物线的解析式为y= x2-
x2-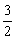 x-2.
x-2.
∴y= (x-
(x-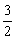 )2-
)2-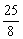 ,
, ∴顶点D的坐标为(
∴顶点D的坐标为(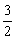 , -
, -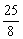 ).
).
(2)当x = 0时,y = -2,∴C(0,-2),OC = 2,
当y = 0时, x2-
x2-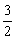 x-2 = 0, ∴x1 = -1, x2 = 4,∴B (4,0),
x-2 = 0, ∴x1 = -1, x2 = 4,∴B (4,0),
∴OA = 1,OB = 4,AB = 5,∵AB2 = 25,AC2 = OA2 + OC2 = 5,BC2 = OC2 + OB2 = 20,
∴AC2 +BC2 = AB2,∴△ABC是直角三角形.
(3)点A关于对称轴的对称 点B, BC交对称轴于点M,根据轴对称性及两点之间线段最短可知,MC + MA的值最小,即△ACM周长最小,
点B, BC交对称轴于点M,根据轴对称性及两点之间线段最短可知,MC + MA的值最小,即△ACM周长最小,
可求直线BC的解析式为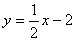 ,∴
,∴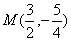 ,△ACM最小周长是
,△ACM最小周长是 .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A( ,3),B(
,3),B(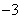 ,1),C(
,1),C(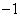 ,3).
,3).
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△AB C关于原点O成中心对称,画出△A2B2C2.
C关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两支仪仗队的队员人数相同,平均身高相同,身高的方差分别为S2甲=0.9,S2乙=1.1,则甲、乙两支仪仗队的队员身高更整齐的是 (填“甲”或“乙”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com