
【题目】如图,在长方形ABCD中,AB=CD=5厘米,AD=BC=4厘米.动点P从A出发,以1厘米/秒的速度沿A→B运动,到B点停止运动;同时点Q从C点出发,以2厘米/秒的速度沿C→B→A运动,到A点停止运动.设P点运动的时间为t秒(t>0),

(1)当点Q在BC边上运动时,t为何值,AP=BQ;
(2)当t为何值时,S△ADP=S△BQD.
【答案】(1)t为![]() 时,AP=BQ;(2)当t=
时,AP=BQ;(2)当t=![]() s或4s后,S△ADP=S△BQD.
s或4s后,S△ADP=S△BQD.
【解析】
(1)分别用含t的式子表示出AP、BQ,根据AP=BQ,可得t的值.
(2)分两种情况讨论,①当点Q在CB上时,②当点Q运动至BA上时,分别表示出△ADP及△BQD的面积,建立方程求解即可.
(1)当点Q在BC边上运动时,
AP=t,BQ=4-2t,
由题意得:t=4-2t,
解得:t=![]() ;
;
即当点Q在BC边上运动时,t为![]() 时,AP=BQ;
时,AP=BQ;
(2)①当点Q在CB上时,
如图1所示:

S△ADP=![]() AD×AP=2t,S△BQD=
AD×AP=2t,S△BQD=![]() BQ×DC=
BQ×DC=![]() (4-2t),
(4-2t),
则2t=![]() (4-2t),
(4-2t),
解得:t=![]() ;
;
②当点Q运动至BA上时,
如图2所示:

S△ADP=![]() AD×AP=2t,S△BQD=
AD×AP=2t,S△BQD=![]() BQ×DA=2(2t-4),
BQ×DA=2(2t-4),
则2t=2(2t-4),
解得:t=4;
综上可得:当t=![]() s或4s后,S△ADP=S△BQD.
s或4s后,S△ADP=S△BQD.


科目:初中数学 来源: 题型:
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
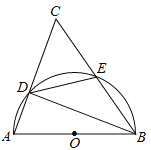
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
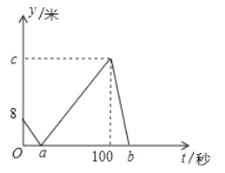
【题目】甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地体息.已知甲先出发![]() ,在跑步过程中,甲、乙两人的距离
,在跑步过程中,甲、乙两人的距离![]() 与乙出发的时间
与乙出发的时间![]() 之间的关系如图所示,给出的下结论:①
之间的关系如图所示,给出的下结论:①![]() ,②
,②![]() ,③
,③![]() ,其中正确的是______.
,其中正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2018个正整数1,2,3,4,…,2018按如图方式排列成一个表.

(1)用如图方式框住表中任意4个数,记左上角的一个数为![]() ,则另三个数用含
,则另三个数用含![]() 的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
(2)用(1)中方式被框住的4个数之和可能等于2019吗?如果可能,请求出![]() 的值;如果不可能,请说明理由.
的值;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“健益”超市购进一批![]() 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以![]() 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出![]() 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量![]() (千克)与销售单价
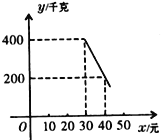
(千克)与销售单价![]() (元)(
(元)(![]() )存在如下图所示的一次函数关系.
)存在如下图所示的一次函数关系.
(1)试求出y与x的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润p元,当销售单价为何值时,每天可获得 最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过4480元,现该超市经理要求每天利润不得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).
查看答案和解析>>
科目:初中数学 来源: 题型:
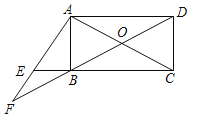
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com