
【题目】某车间一周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +5 | ﹣5 | +5 | +10 | ﹣10 | ﹣15 |
(1)本周三生产了多少辆电动车?
(2)本周总产量与计划总生产量相比,是增加多少辆?还是减少多少辆?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
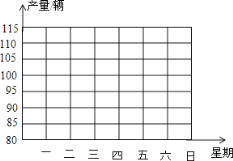
(4)请你用折线图画出电动车产量的变化情况.
【答案】(1)95辆;(2)减少15辆;(3)25辆 ;(4)见解析
【解析】
(1)根据表格列出算式,计算即可得到结果;
(2)表格中的数据相加得到结果,即可做出判断;
(3)找出产量最多与最少的,相减即可得到结果;
(4)根据表格中的数据先求出本周每天的产量,再画出折线统计图即可.
(1)本周三生产的电动车数量为:100+(-5)=95(辆);
(2)根据题意得:
(-5)+5+(-5)+5+10+(-10)+(-15)=-15,
则本周总产量与计划总生产量相比,减少了15辆;
(3)产量最多的一天比产量最少的一天多生产(+10)-(-15)=25(辆),
则产量最多的一天比产量最少的一天多生产了25辆;
(4)本周每天的产量为:
星期一:100+(-5)=95(辆),星期二:100+(+5)=105(辆),
星期四:100+(+5)=105(辆),星期五:100+(+10)=110(辆),
星期六:100+(-10)=90(辆),星期日:100+(-15)=85(辆),
折线图如下:


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
【题目】“红树林小组”全体组员参加了义务植树活动,领得准备种植的树苗一批,组长决定采用分工负责制,经计算发现:若每位组员种植10棵树苗,则还剩88棵;若每位组员种植12棵树苗,则有一位组员种植的树苗不到4棵,求准备种植树苗的棵数和“红树林小组”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
这条分割直线既平分了三角形的面积,又平分了三角形的周长,我们称这条直线为三角形的“等分积周线”.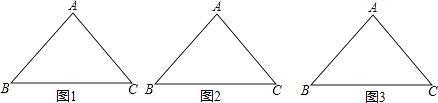
(1)小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).
(2)小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.
(3)若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能找出规律吗?
(1)计算:![]() ×
×![]() =________,
=________,![]() =________;
=________;![]() ×
×![]() =________,
=________,![]() =________.
=________.
(2)请按找到的规律计算:
①![]() ×
×![]() ;
;
②![]() ×
×![]() .
.
(3)已知a=![]() ,b=
,b=![]() ,用含a,b的式子表示
,用含a,b的式子表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
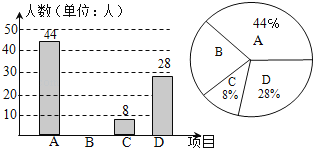
【题目】我区积极开展“体育大课间”活动,引导学生坚持体育锻炼.某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;
(2)请把条形统计图补充完整;
(3)已知该校有1000人,请根据样本估计全校最喜欢足球的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
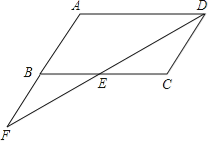
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为BC边上的点(不与B,C重合),F为CD边上的点(不与C,D重合),且AE=AF,AB=4,设△AEF的面积为y,EC的长为x,求y关于x的函数关系式,并写出自变量x的取值范围.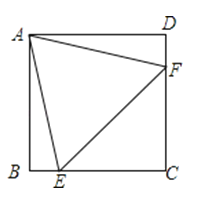
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com