
【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
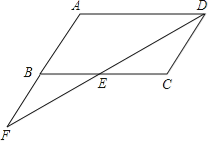
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC
∴∠CDE=∠F
又∵BF=AB
∴DC=FB
在△DCE和△FBE中,
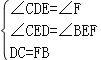
∴△DCE≌△FBE(AAS)
(2)解:∵△DCE≌△FBE,
∴EB=EC,
∵EC=3,
∴BC=2EB=6
∵四边形ABCD是平行四边形,
∴AD=BC=6.
【解析】试题分析:(1)由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∠CDE=∠F,又由BF=AB,即可利用AAS,判定△DCE≌△FBE;
(2)由(1),可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠CDE=∠F,
又∵BF=AB,
∴DC=FB,
在△DCE和△FBE中,
∵![]()
∴△DCE≌△FBE(AAS)
(2)解:∵△DCE≌△FBE,
∴EB=EC,
∵EC=3,
∴BC=2EB=6,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴AD=6.


科目:初中数学 来源: 题型:
【题目】等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2012次后,点B( )
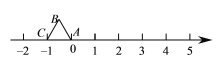
A. 不对应任何数 B. 对应的数是2010 C. 对应的数是2011 D. 对应的数是2012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间一周内计划每天生产100辆电动车,由于工人实行轮休,每天上班人数不一定相等,实际每天生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | ﹣5 | +5 | ﹣5 | +5 | +10 | ﹣10 | ﹣15 |
(1)本周三生产了多少辆电动车?
(2)本周总产量与计划总生产量相比,是增加多少辆?还是减少多少辆?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
(4)请你用折线图画出电动车产量的变化情况.
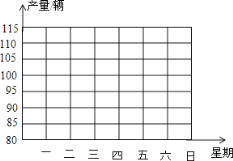
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系中,A(-1,-3),OB=![]() ,OB与x轴所夹锐角是45°
,OB与x轴所夹锐角是45°
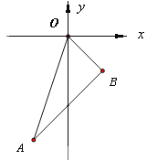
(1)求B点坐标
(2)判断三角形ABO的形状
(3)求三角形ABO的AO边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图中的图象(折线![]() )描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为![]() 千米/时;
千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】符号“f”表示一种运算,它对一些数的运算如下:f(1)=1+![]() ,f(2)=1+
,f(2)=1+![]() ,f(3)=1+
,f(3)=1+![]() ,f(4)=1+
,f(4)=1+![]() …
…
(1)利用以上运算规律,写出f(2017)=__________;
(2)计算:f(1)f(2)f(3)…f(100)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道简便计算的好处,事实上,简便计算在好多地方都存在,观察下列等式:
![]() ,
,![]() ,
,![]() ,…
,…
![]() 根据上述格式反应出的规律填空:
根据上述格式反应出的规律填空:![]() ________;
________;
![]() 设这类等式左边两位数的十位数字为
设这类等式左边两位数的十位数字为![]() ,请用一个含
,请用一个含![]() 的代数式表示其结果;
的代数式表示其结果;
![]() 这种简便计算也可以推广应用:个位数字是
这种简便计算也可以推广应用:个位数字是![]() 的三位数的平方,请写出
的三位数的平方,请写出![]() 的简便计算过程及结果.
的简便计算过程及结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线l1:y=![]() (x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
A.y=![]() (x﹣2)2+4
(x﹣2)2+4
B.y=![]() (x﹣2)2+3
(x﹣2)2+3
C.y=![]() (x﹣2)2+2
(x﹣2)2+2
D.y=![]() (x﹣2)2+1
(x﹣2)2+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com