
【题目】已知如图,在平面直角坐标系中,A(-1,-3),OB=![]() ,OB与x轴所夹锐角是45°
,OB与x轴所夹锐角是45°
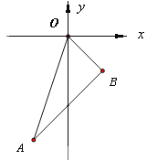
(1)求B点坐标
(2)判断三角形ABO的形状
(3)求三角形ABO的AO边上的高.
【答案】(1)B(1,-1);(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)根据题中给出的条件在平面直角坐标系中,A(-1,-3),OB=![]() ,OB与x轴所夹锐角是45°那么由点B作x轴的垂线交x轴与点C,那么就可以知道三角形OBC为等腰直角三角形,根据勾股定理可以求出BC=OC的长度,即可求得点B坐标;(2)根据地(1)中求出点B的坐标之后可以求出线段OB,AB,的长度,那么运用勾股定理逆定理可以判断出三角形ABO为直角三角形;(3)第三问求高度问题那么就需要求出三角形ABO的面积,那么根据面积就可以求得AO边上的高.
,OB与x轴所夹锐角是45°那么由点B作x轴的垂线交x轴与点C,那么就可以知道三角形OBC为等腰直角三角形,根据勾股定理可以求出BC=OC的长度,即可求得点B坐标;(2)根据地(1)中求出点B的坐标之后可以求出线段OB,AB,的长度,那么运用勾股定理逆定理可以判断出三角形ABO为直角三角形;(3)第三问求高度问题那么就需要求出三角形ABO的面积,那么根据面积就可以求得AO边上的高.
试题解析:解(1)过点B作x轴的垂线交x轴与点C,如图所示:
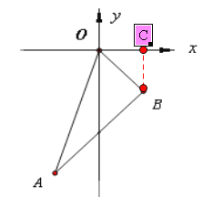
那么根据已知条件![]() ,所以在
,所以在![]() 中根据勾股定理可知
中根据勾股定理可知![]()
因为点B在第四象限,所以点B坐标为(1,-1)
(2)根据上面求得点B的坐标可知OA=![]() ,AB=
,AB=![]()
那么就有![]() 所以三角形ABO为直角三角形;
所以三角形ABO为直角三角形;
(3)因为三角形ABO为直角三角形,所以
![]() , h=
, h=![]()


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】某社区从2011年开始,组织全民健身活动,结合社区条件,开展了广场舞、太极拳、羽毛球和跑步四个活动项目,现将参加项目活动总人数进行统计,并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图,请你根据统计图解答下列题
(1)2015年比2011年增加 人;
(2)请根据扇形统计图求出2015年参与跑步项目的人数;
(3)组织者预计2016年参与人员人数将比2015年的人数增加15%,名各活动项目参与人数的百分比与2016年相同,请根据以上统计结果,估计2016年参加太极拳的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
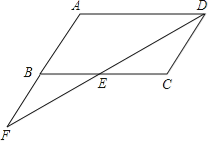
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式:﹣x,3x2,﹣5x3,7x4,…,﹣37x19,39x20,…,写出第n(n为正整数)个单项式,为解决这个问题,特提供下面的解题思路:
(1)这组单项式的系数的符号规律是 ,系数的绝对值规律是 ;
(2)这组单项式的次数的规律是 ;
(3)根据上面的归纳,可以猜想第n(n为正整数)个单项式吗;
(4)请你根据猜想,写出第2017个、第2018个单项式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 y=![]() (a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
(a为常数)的图象上有三点(﹣4,y1),(﹣1,y2),(2,y3),则函数值y1 , y2 , y3的大小关系是( )
A.y3<y1<y2
B.y3<y2<y1
C.y1<y2<y3
D.y2<y3<y1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com