
【题目】已知抛物线c:y=-x2-2x+3和直线l:y=![]() x+d。将抛物线c在x轴上方的部分沿x轴翻折180°,其余部分保持不变,翻折后的图象与x轴下方的部分组成一个“M”型的新图象(即新函数m:y=-|x2+2x-3|的图象)。
x+d。将抛物线c在x轴上方的部分沿x轴翻折180°,其余部分保持不变,翻折后的图象与x轴下方的部分组成一个“M”型的新图象(即新函数m:y=-|x2+2x-3|的图象)。
(1)当直线l与这个新图象有且只有一个公共点时,d= ;
(2)当直线l与这个新图象有且只有三个公共点时,求d的值;
(3)当直线l与这个新图象有且只有两个公共点时,求d的取值范围;
(4)当直线l与这个新图象有四个公共点时,直接写出d的取值范围.
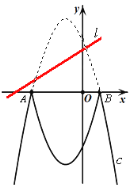
【答案】(1)d=![]() ;(2)d=
;(2)d=![]() 或d=
或d=![]() (3)
(3)![]() <d<
<d<![]() 或d<
或d<![]() ; (4)
; (4)![]() <d<
<d<![]() 。
。
【解析】
(1)令-x2-2x+3=![]() x+d求解即可;
x+d求解即可;
(2)设抛物线c:y=-x2-2x+3与x轴交于点A(-3,0),点B(1,0),则根据方程有两个相等的实根求出P的坐标,然后求解即可;
(3)(4)根据(2)求出的P点坐标进行数形结合画图找出d的取值范围即可.
解:(1)当直线l经过点A(-3,0)时,d=![]() ;
;
(2)设抛物线c:y=-x2-2x+3与x轴交于点A(-3,0),点B(1,0),
直线l:y=![]() x+d与抛物线c:y=x2+2x-3(-3<x<1)相切于点P,则点P的横坐标恰好是方程
x+d与抛物线c:y=x2+2x-3(-3<x<1)相切于点P,则点P的横坐标恰好是方程![]() x+d=x2+2x-3,即2x2+3x-2d-6=0(-3<x<1)的两个相等实数根,解△=9+8(2d+6)=0得d=
x+d=x2+2x-3,即2x2+3x-2d-6=0(-3<x<1)的两个相等实数根,解△=9+8(2d+6)=0得d=![]() ,
,
∴点P的坐标为(![]() ).
).
①当直线l经过点B(1,0)时,直线l与这个新图象有且只有三个公共点,解得d=![]() ;
;
②当直线l经过点P(![]() )时,直线l与这个新图象有且只有三个公共点,解得d=
)时,直线l与这个新图象有且只有三个公共点,解得d=![]() ;
;
∴综合①、②得:d=![]() 或d=
或d=![]()
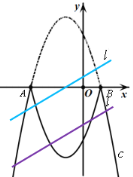
(3)①由平移直线l可得:直线l从经过点A(-3,0)开始向下平移到直线l经过点P(![]() )的过程中,直线l与这个新图象有且只有两个公共点,可得
)的过程中,直线l与这个新图象有且只有两个公共点,可得![]() <d<
<d<![]()
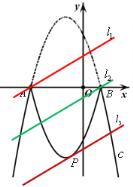
②直线l从经过点P(![]() )继续向下平移的过程中,直线l与这个新图象有且只有两个公共点,可得d<
)继续向下平移的过程中,直线l与这个新图象有且只有两个公共点,可得d<![]() ;
;
∴综合①、②得:![]() <d<
<d<![]() 或d<
或d<![]() ;
;
(4)如图:当直线l经过点B(1,0)时,直线l与这个新图象有且只有三个公共点,解得d=![]() ;
;
当直线l继续向下平移的过程中经过点P(![]() ),直线l与这个新图象有且只有三个公共点,可得d=
),直线l与这个新图象有且只有三个公共点,可得d=![]() ;
;
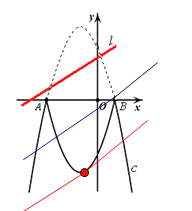
∴要使直线l与这个新图象有四个公共点则d的取值范围是![]() <d<
<d<![]() .
.


科目:初中数学 来源: 题型:
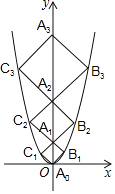
【题目】二次函数y=x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…n在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnn都是正方形,则正方形An﹣1BnAnn的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
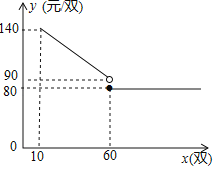
【题目】立定跳远是嘉兴市体育中考的抽考项目之一,某校九年级(1),(2)班准备集体购买某品牌的立定跳远训练鞋.现了解到某网店正好有这种品牌训练鞋的促销活动,其购买的单价y(元/双)与一次性购买的数量x(双)之间满足的函数关系如图所示.
(1)当10≤x<60时,求y关于x的函数表达式;
(2)九(1),(2)班共购买此品牌鞋子100双,由于某种原因需分两次购买,且一次购买数量多于25双且少于60双;
①若两次购买鞋子共花费9200元,求第一次的购买数量;
②如何规划两次购买的方案,使所花费用最少,最少多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
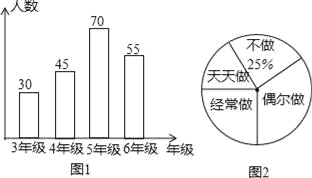
【题目】“热爱劳动,勤俭节约”是中华民族的光荣传统,某小学校为了解本校3至6年级的3000名学生帮助父母做家务的情况,以便做好引导和教育工作,随机抽取了200名学生进行调查,按年级人数和做家务程度,分别绘制了条形统计图(图1)和扇形统计图(图2).
(1)四个年级被调查人数的中位数是多少?
(2)如果把“天天做”、“经常做”、“偶尔做”都统计成帮助父母做家务,那么该校3至6年级学生帮助父母做家务的人数大约是多少?
(3)在这次调查中,六年级共有甲、乙、丙、丁四人“天天帮助父母做家务”,现准备从四人中随机抽取两人进行座谈,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
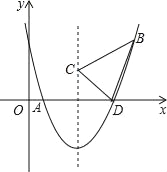
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点,并经过B点,已知A点坐标是(2,0),B点坐标是(8,6).
(1)求二次函数的解析式;
(2)求函数图象的顶点坐标及D点的坐标;
(3)二次函数的对称轴上是否存在一点C,使得△CBD的周长最小?若C点存在,求出C点的坐标;若C点不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
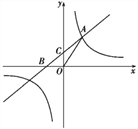
【题目】如图15,直线y=x+b与双曲线y=![]() 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠BCD=90°,ABCD=BCBD,BM∥CD交AD于点M.连接CM交DB于点N.
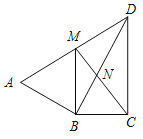
(1)求证:△ABD∽△BCD;
(2)若CD=6,AD=8,求MC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com