
【题目】定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.
(1)直接写出等腰直角三角形腰上的中高比为 .
(2)已知一个直角三角形一边上的中高比为5:4,求它的最小内角的正切值.
(3)如图,已知函数y= ![]() (x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.
(x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.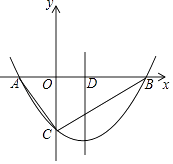
【答案】
(1)![]()
(2)
解:①当斜边上的中高比为5:4时,设高线为4k,则此边上的中线为5k,如图2,
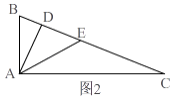
在△ABC中,∠BAC=90°,
∴AD是高,
∴AD=4x,AE是中线,
∴CE=AE=5x,
在RtADE中,DE= ![]() =3k,
=3k,
∴CD=CE+DE=8k,
∴tan∠C= ![]() =
= ![]() =
= ![]() ,
,
当直角边上的中高比为5:4时,设高为4k,此边上的中线为5k,
如图3,
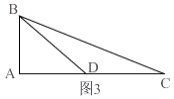
在△ABC中,∠BAC=90°,AB是AC边上的高,为4k,BD为AC边上的中线,为5k,
根据勾股定理得,AD= ![]() =3k,
=3k,
∴AC=2AD=6k,
∴tan∠C= ![]() =
= ![]() ,
,
∴直角三角形的最小内角的正切值为 ![]() 或
或 ![]() ;
;
(3)
解:∵函数y= ![]() (x+4)(x﹣m)与x轴交于A、B两点,
(x+4)(x﹣m)与x轴交于A、B两点,
∴令y=0,∴0= ![]() (x+4)(x﹣m),
(x+4)(x﹣m),
∴x=﹣4或x=m,
∴A(﹣4,0),B(m,0),
∵点C是抛物线与y轴的交点,
∴C(0,﹣ ![]() ),
),
∵对称轴与x的正半轴交于点D,
∴D( ![]() ,0),
,0),
在Rt△COD中,设CD=5k,
∴OC=4k,
根据勾股定理得,OD=3k,
∴ 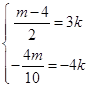 ,∴
,∴ ![]() ,
,
即m的值为10.
【解析】解:(1)如图1,
设等腰直角三角形的直角边为2x,
∴BC边上的高为AB=2x,
∵AD是BC边上的中线,
∴BD= ![]() BC=x,
BC=x,
在Rt△ABD中,根据勾股定理得,AD= ![]() =
= ![]() x,
x,
∴等腰直角三角形腰上的中高比为 ![]() =
= ![]() ,
,
所以答案是: ![]() ;
;


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,BD是对角线. 
(1)求证:△ADE≌△CBF;
(2)若∠ADB是直角,请证明四边形BEDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题![]() ,小虎马上举手,要求到黑板上去做,他是这样做的:
,小虎马上举手,要求到黑板上去做,他是这样做的:
5(3x-1)=2(4x+2)-1①,
15x-5=8x+4-1②,
15x-8x=4-1+5③
7x④,
x=![]() ⑤
⑤
老师说:小虎解一元一次方程的一般步骤都知道,但没有掌握好,因此解题出现了错误,请指出他的错步及错误原因: ,方程的正确的解是x= .
然后,你自己细心的解下面的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2﹣3(m+1)x+2m+3=0
(1)如果该方程有两个不相等的实数根,求m的取值范围;
(2)在(1)的条件下,当该方程的根都是整数,且|x|<4时,求m的整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题小组为了解某品牌手机的销售情况,对某专卖店该品牌手机在今年1~4月的销售做了统计,并绘制成如图两幅统计图(如图). 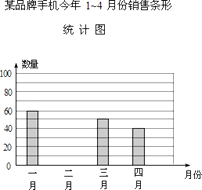

(1)该专卖店1~4月共销售这种品牌的手机台;
(2)请将条形统计图补充完整;
(3)在扇形统计图中,“二月”所在的扇形的圆心角的度数是;
(4)在今年1~4月份中,该专卖店售出该品牌手机的数量的中位数是台.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OA⊥OB,OA=4,OB=3,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E. 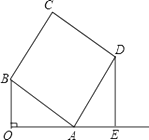
(1)证明:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?请说明理由,并求出此时点C到OE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为cm.(结果保留π) 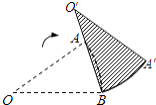
查看答案和解析>>
科目:初中数学 来源: 题型:
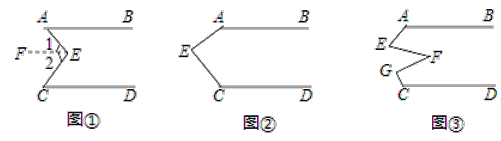
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com