
【题目】如图,已知OA⊥OB,OA=4,OB=3,以AB为边作矩形ABCD,使AD=a,过点D作DE垂直OA的延长线交于点E. 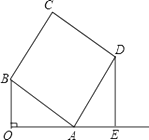
(1)证明:△OAB∽△EDA;
(2)当a为何值时,△OAB与△EDA全等?请说明理由,并求出此时点C到OE的距离.
【答案】
(1)证明:如图所示,
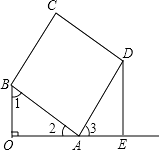
∵OA⊥OB,
∴∠1+∠2=90°,
又∵四边形ABCD是矩形,
∴∠BAD=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
∵OA⊥OB,OE⊥OA,
∴∠BOA=∠DEA=90°,
∴△OAB∽△EDA.
(2)解:在Rt△OAB中,AB= ![]() =5,
=5,
由(1)可知∠1=∠3,∠BOA=∠DEA=90°,
∴当a=AD=AB=5时,△AOB与△EDA全等.
当a=AD=AB=5时,可知矩形ABCD为正方形,
∴BC=AB,如图,过点C作CH⊥OE交OE于点H,
则CH就是点C到OE的距离,过点B作BF⊥CH交CH于点F,
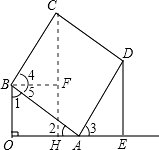
则∠4与∠5互余,∠1与∠5互余,
∴∠1=∠4,
又∵∠BFC=∠BOA,BC=AB,
∴△OAB≌△FCB(AAS),
∴CF=OA=4,BO=BF.
∴四边形OHFB为正方形,
∴HF=OB=3,
∴点C到OE的距离CH=CF+HF=4+3=7.
【解析】(1)由于四边形ABCD是矩形,则∠BAD=90°,那么∠OBA、∠DAE同为∠BAO的余角,即∠OBA=∠DAE,而∠BOA、∠DEA都是直角,由此可证得△OAB∽△EDA.(2)若△OAB与△EDA全等,则AB=AD,在Rt△OAB中,利用勾股定理易求得AB=5,那么a=AD=AB=5; 求C到OE的距离,可过C作CH⊥OE于H,过B作BF⊥CH于F;那么CH就是所求的距离,通过上面的解题思路,易证得△CBF≌△ABO,得CH=OA=4,BO=BF,那么四边形BOHF是正方形,由此可得FH=BO=3,根据CH=CF+FH即可求得C到OE的距离.
【考点精析】通过灵活运用矩形的性质和相似三角形的判定,掌握矩形的四个角都是直角,矩形的对角线相等;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】解方程:![]() (x-2)-
(x-2)-![]() (4x-1)=4.
(4x-1)=4.
【答案】x=-![]() .
.
【解析】
方程两边都乘以6去分母后,去括号,移项合并,将x系数化为1即可求出解.
去分母得:3(x-2)-2(4x-1)=24,
去括号得:3x-6-8x+2=24,
移项合并得:-5x=28,
解得:x=-![]() .
.
【点睛】
此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将x系数化为1,求出解.
【题型】解答题
【结束】
22
【题目】(1)已知a+b=5,ab=-2,求代数式(6a-3b-2ab)-(a-8b-ab)的值;
(2)已知2x-y-4=0,求9x27y÷81y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)8﹣(﹣2)
(2)1﹣6+(﹣20)﹣(﹣5)
(3)﹣4×(﹣3)2+5×(﹣2)﹣6
(4)(1﹣![]() +
+![]() )×(﹣48)
)×(﹣48)
(5)﹣22+[(﹣4)2﹣(1﹣3)×3]
(6)(﹣125![]() )÷(﹣5)
)÷(﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.
(1)直接写出等腰直角三角形腰上的中高比为 .
(2)已知一个直角三角形一边上的中高比为5:4,求它的最小内角的正切值.
(3)如图,已知函数y= ![]() (x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.
(x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.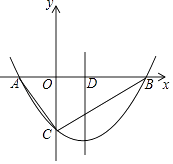
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个白色六边形相邻.若一段边框上有45个黑色六边形,则这段边框共有白色六边形( )
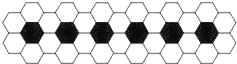
A. 182个 B. 180个 C. 272个 D. 270个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3 ![]() ,MN=2
,MN=2 ![]() .
. 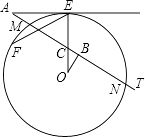
(1)求∠COB的度数;
(2)求⊙O的半径R;
(3)点F在⊙O上( ![]() 是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧 ![]() 的中点,连接AE交BC于点F,若cosC=
的中点,连接AE交BC于点F,若cosC= ![]() ,AC=6,则BF的长为 .
,AC=6,则BF的长为 . 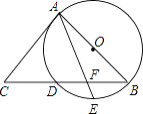
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com