练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB为⊙O的内接正多边形的一边，已知∠OAB=70°，则这个正多边形的内角和为 ．

    【答案】1260°
    【解析】解：∵OA=OB， ∴∠OAB=∠OBA=70°，
    ∴∠AOB=40°，
    ∵AB为⊙O的内接正多边形的一边，
    ∴正多边形的边数= =9，
    ∴这个正多边形的内角和=（9﹣2）×180°=1260°，
    所以答案是：1260°．
    【考点精析】解答此题的关键在于理解多边形内角与外角的相关知识，掌握多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°，以及对正多边形和圆的理解，了解圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，已知AD∥BC，∠B=90°，AB=7，AD=9，BC=12，在线段BC上任取一点E，连接DE，作EF⊥DE，交直线AB于点F．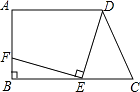
    （1）若点F与B重合，求CE的长；
    （2）若点F在线段AB上，且AF=CE，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：(x-2)-(4x-1)=4.

    【答案】x=-.

    【解析】

    方程两边都乘以6去分母后，去括号，移项合并，将x系数化为1即可求出解.

    去分母得：3（x-2）-2（4x-1）=24，

    去括号得：3x-6-8x+2=24，

    移项合并得：-5x=28，

    解得：x=-.

    【点睛】

    此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将x系数化为1，求出解．

    【题型】解答题
    【结束】
    22

    【题目】（1）已知a+b=5，ab=-2，求代数式（6a-3b-2ab）-（a-8b-ab）的值；

    （2）已知2x-y-4=0，求9x27y÷81y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图1是由5个完全相同的正方体搭成的几何体，现将标有E的正方体平移至图2所示的位置，下列说法中正确的是（ ）
    ①左、右两个几何体的主视图相同
    ②左、右两个几何体的俯视图相同
    ③左、右两个几何体的左视图相同．

    A.①②③
    B.②③
    C.①②
    D.①③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1）是一个六角星的纸板，其中六个锐角都为60°，六个钝角都为120°，每条边都相等，现将该纸板按图（2）切割，并无缝隙无重叠地拼成矩形ABCD．若六角星纸板的面积为9 cm2 ， 则矩形ABCD的周长为（ ）
    A.18cm
    B.8 cm
    C.（2 +6）cm
    D.（6 +6）cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠ACB=90°，AC=BC，AB=2，现将一块三角板的直角顶点放在AB的中点D处，两直角边分别与直线AC，直线BC相交于点E，F，我们把DE⊥AC时的位置定为起始位置（如图1），将三角板绕点D顺时针方向旋转一个角度α（0°＜α＜90°）．

    （1）如图2，在旋转过程中，当点E在线段AC上时，试判别△DEF的形状，并说明理由；

    （2）设直线ED交直线BC于点G，在旋转过程中，是否存在点G，使得△EFG为等腰三角形？若存在，求出CG的长，若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算

    （1）8﹣（﹣2）

    （2）1﹣6+（﹣20）﹣（﹣5）

    （3）﹣4×（﹣3）2+5×（﹣2）﹣6

    （4）（1﹣+）×（﹣48）

    （5）﹣22+[（﹣4）2﹣（1﹣3）×3]

    （6）（﹣125）÷（﹣5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：三角形一边的中线与这边上的高线之比称为这边上的中高比．
    （1）直接写出等腰直角三角形腰上的中高比为 ．
    （2）已知一个直角三角形一边上的中高比为5：4，求它的最小内角的正切值．
    （3）如图，已知函数y= （x+4）（x﹣m）与x轴交于A、B两点，与y轴的负半轴交于点C，对称轴与x的正半轴交于点D，若△ABC中AB边上的中高比为5：4，求m的值．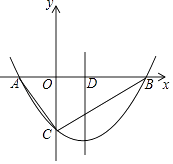

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知∠EAT=30°，AE=3 ，MN=2 ．
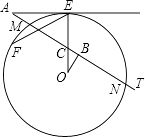
    （1）求∠COB的度数；
    （2）求⊙O的半径R；
    （3）点F在⊙O上（ 是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．

    查看答案和解析>>

    同步练习册答案