
【题目】已知关于x的一元二次方程mx2﹣3(m+1)x+2m+3=0
(1)如果该方程有两个不相等的实数根,求m的取值范围;
(2)在(1)的条件下,当该方程的根都是整数,且|x|<4时,求m的整数值.
【答案】(1)m的取值范围为m≠0和m≠﹣3;(2)m的值为﹣1或3.
【解析】
(1)由方程根的情况,根据根的判别式可得到关于m的不等式,则可求得m的取值范围;
(2)令mx2﹣3(m+1)x+2m+3=0,表示出x,根据该方程的根都是整数,求出整数![]() 的值,根据x的范围即可确定出m的整数值.
的值,根据x的范围即可确定出m的整数值.
解:(1)由题意m≠0,
∵方程有两个不相等的实数根,
∴△>0,即[﹣3(m+1)]2﹣4m(2m+3)=(m+3)2>0,
解得:m≠﹣3,
则m的取值范围为m≠0和m≠﹣3;
(2)设y=0,则mx2﹣3(m+1)x+2m+3=0.
∵△=(m+3)2,
∴![]()
∴![]()
当![]() 是整数时,可得m=1或m=﹣1或m=3,
是整数时,可得m=1或m=﹣1或m=3,
∵|x|<4,m=1不合题意舍去,
∴m的值为﹣1或3.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车的速度为100千米/时,乙车的速度为80千米/时,___________小时后两车相距30千米.
【答案】![]() 或
或![]()
【解析】
应该有两种情况,第一次应该还没相遇时相距30千米,第二次应该是相遇后交错离开相距30千米,根据路程=速度×时间,可列方程求解.
设第一次相距30千米时,经过了x小时,
由题意,得(100+80)x=450-30,
解得x=![]() ;
;
设第二次相距30千米时,经过了y小时,
由题意,得(100+80)y=450+30,
解得y=![]() ,
,
故经过![]() 小时或
小时或![]() 小时相距30千米.
小时相距30千米.
故答案为:![]() 或
或![]()
【点睛】
本题考查理解题意能力,关键知道相距30千米时有两次以及知道路程=速度×时间,以路程做为等量关系可列方程求解.
【题型】填空题
【结束】
18
【题目】如图,一个长方体的表面展开图中四边形ABCD是正方形(正方形的四个角都是直角、四条边都相等),则根据图中数据可得原长方体的体积是_________cm3.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一个六角星的纸板,其中六个锐角都为60°,六个钝角都为120°,每条边都相等,现将该纸板按图(2)切割,并无缝隙无重叠地拼成矩形ABCD.若六角星纸板的面积为9 ![]() cm2 , 则矩形ABCD的周长为( )
cm2 , 则矩形ABCD的周长为( ) 
A.18cm
B.8 ![]() cm
cm
C.(2 ![]() +6)cm
+6)cm
D.(6 ![]() +6)cm
+6)cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)8﹣(﹣2)
(2)1﹣6+(﹣20)﹣(﹣5)
(3)﹣4×(﹣3)2+5×(﹣2)﹣6
(4)(1﹣![]() +
+![]() )×(﹣48)
)×(﹣48)
(5)﹣22+[(﹣4)2﹣(1﹣3)×3]
(6)(﹣125![]() )÷(﹣5)
)÷(﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
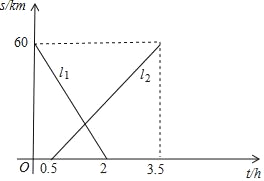
【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填![]() 或
或![]() );
);
(2)甲的速度是 km/h,乙的速度是 km/h;
(3)甲出发多少小时两人恰好相距5km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三角形一边的中线与这边上的高线之比称为这边上的中高比.
(1)直接写出等腰直角三角形腰上的中高比为 .
(2)已知一个直角三角形一边上的中高比为5:4,求它的最小内角的正切值.
(3)如图,已知函数y= ![]() (x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.
(x+4)(x﹣m)与x轴交于A、B两点,与y轴的负半轴交于点C,对称轴与x的正半轴交于点D,若△ABC中AB边上的中高比为5:4,求m的值.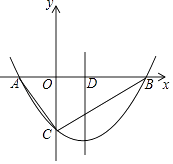
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(1)班的宣传委员在办黑板报时,采用了下面的图案作为边框,其中每个黑色六边形与6个白色六边形相邻.若一段边框上有45个黑色六边形,则这段边框共有白色六边形( )
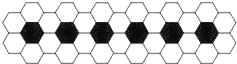
A. 182个 B. 180个 C. 272个 D. 270个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=﹣x﹣4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为﹣2 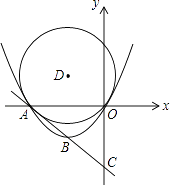
(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连结AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com